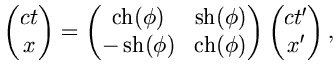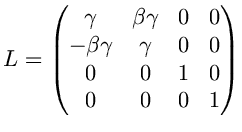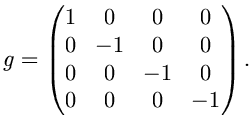Физика
Современные физические концепции
Следующий раздел: 1.4 Сокращение длины Выше по контексту: 1. Специальная Теория Относительности Предыдущий раздел: 1.2 Постулаты СТО Алфавитный
индекс
Разделы
- 1.3.1 Мировая точка, мировая линия, сигнал
- 1.3.2 Интервал
- 1.3.3 Пространство Минковского, инвариантность интервала
- 1.3.4 Поворот в пространстве Минковского, матрица Лоренца
- 1.3.5 Общепринятые обозначения
- 1.3.6 Группа Лоренца, группа Пуанкаре
1. Специальная Теория Относительности
1.3 Математический аппарат СТО
Из постулатов мы можем формально вывести все остальные положения СТО. Для этого надо сначала ввести некоторые понятия:
1.3.1 Мировая точка, мировая линия, сигнал
Будем называть мировой точкой четыре величины: время и три пространственные координаты. Мировой линией будем называть непрерывную линию мировых точек. Очевидно, движение материальной точки может быть представлено в виде мировой линии. Если с мировой точкой происходит какое-то "событие", способное повлиять на другие точки, считаем, что она посылает "сигнал". Сигнал распространяется с максимальной скоростью распространения взаимодействия (сигнала). Иногда инвариантность максимальной скорости распространения взаимодействия выносят в отдельный постулат, но вообще-то в этом особого смысла нет -- это есть следствие принципа относительности и того экспериментального факта, что скорость распространения взаимодействия конечна (N.B.: о ее предельности пока речи нет).
1.3.2 Интервал
Сигнал проходит за малое время ![]() расстояние
расстояние
![]() . При этом
пространственные координаты изменились на
. При этом
пространственные координаты изменились на ![]() ,
, ![]() и
и ![]() . Следовательно,
. Следовательно,
![]() (по теореме
Пифагора, ибо малое перемещение мы можем считать прямолинейным)
или же,
(по теореме
Пифагора, ибо малое перемещение мы можем считать прямолинейным)
или же,
![]() . Теперь,
пусть
. Теперь,
пусть ![]() ,
,![]() ,
,![]() ,
,![]() -- расстояние
между двумя произвольными близкими событиями. Введем интервал:
-- расстояние
между двумя произвольными близкими событиями. Введем интервал:
Так как скорость распространения сигнала c не зависит от системы отсчета, нулевой в какой-то системе отсчета интервал (соответствующий событиям испускания и принятия сигнала) будет равен нулю и в любой другой ИСО.
1.3.3 Пространство Минковского, инвариантность интервала
Выражение 1
было бы похоже на квадрат длины вектора в 4х-мерном евклидовом пространстве,
если бы не знаки. Однако, мы можем ввести пространство, в котором
длина вектора определяется именно таким выражением. Это псевдоевклидово
пространство Минковского. Забегая вперед, скажем, что оно характеризуется
следующей метрикой: (+1 -1 -1 -1).
Позволим себе небольшое лирическое отступление: использование понятия о 4х-мерном пространстве Минковского не несет в себе никакой глубокой философской истины. Оно вводится просто как математическая сущность, сильно упрощающая запись многих выражений. То есть, нет смысла говорить, что "мы живем в 4х-мерном пространстве-времени, да еще с неевклидовой метрикой" -- это будет пустое словоблудие. Не нужно пытаться что-то себе представить, не нужно призывать "здравый смысл" -- математическая модель (даже не модель, а просто система обозначений) в подобных духовных упражнениях не нуждается.
Рассмотрим значение интервала в двух разных ИСО: ![]() и
и ![]() .
. ![]() и
и ![]() , очевидно,
являются бесконечно малыми одного порядка, и, соответственно, мы
можем сказать
, очевидно,
являются бесконечно малыми одного порядка, и, соответственно, мы
можем сказать
![]() , где
, где
![]() -- некоторая функция, не зависящая от
-- некоторая функция, не зависящая от ![]() . Более того, a есть функция только относительной скорости систем отсчета,
в которых измерены
. Более того, a есть функция только относительной скорости систем отсчета,
в которых измерены ![]() и
и ![]() (назовем
ее
(назовем
ее ![]() ). Это
утверждение очевидно -- от координат и времени a зависеть не может,
ибо это противоречило бы постулату о равнозначности всех точек пространства-времени.
Далее, a не может зависеть и от направления
). Это
утверждение очевидно -- от координат и времени a зависеть не может,
ибо это противоречило бы постулату о равнозначности всех точек пространства-времени.
Далее, a не может зависеть и от направления ![]() -- иначе
мы бы приняли существование выделенного направления в пространстве.
-- иначе
мы бы приняли существование выделенного направления в пространстве.
Определим вид функции ![]() . Для
этого рассмотрим три ИСО:
. Для
этого рассмотрим три ИСО: ![]() ,
, ![]() ,
, ![]() . Соответственно,
интервал в
. Соответственно,
интервал в ![]() --
-- ![]() , в
, в ![]() он будет
он будет
![]() , в
, в
![]() , и, так
же,
, и, так
же,
![]() , или,
, или,
![]() . Отсюда
немедленно получаем:
. Отсюда
немедленно получаем:
![]() . Последовательно
поменяв местами индексы у
. Последовательно
поменяв местами индексы у ![]() ,
, ![]() ,
, ![]() , получим
систему уравнений, имеющую однозначное решение:
, получим
систему уравнений, имеющую однозначное решение: ![]() . То есть,
. То есть,
![]() .
.
Полученный результат об инвариантности интервала мы можем считать формальной математической записью постулатов СТО. Этой удобной, сжатой формой мы и будем пользоваться в дальнейшем, не аппелируя более к выраженным в словесной форме постулатам в п.1.2.
1.3.4 Поворот в пространстве Минковского, матрица Лоренца
Теперь получим вид преобразований временной и пространственных координат при переходе в другую ИСО.
Как было определено ранее, интервал мы можем рассматривать, как
квадрат длины некоторого вектора в пространстве Минковского.
Назовем этот вектор 4-вектором координат. Преобразование такого
вектора при переходе от одной ИСО к другой должно иметь такой вид,
чтобы длины (расстояния) в пространстве Минковского сохранялись.
По аналогии с известными нам преобразованиями в евклидовом пространстве,
назовем это поворотом (ибо в евклидовом пространстве преобразованием,
происходящим без изменения расстояний, и при этом более сложным,
чем простой параллельный перенос, является поворот). Далее будем
рассматривать поворот в одной плоскости, то есть, поворот, затрагивающий
только 2 координаты из 4х, ибо, очевидно, любой сложный поворот
можно разложить на несколько простых. Так же, отбросим чисто пространственные
повороты, не затрагивающие 0-ю координату (![]() ). И так,
получим выражение для поворота компонент вектора
). И так,
получим выражение для поворота компонент вектора ![]() и
и ![]() вокруг
начала координат. Очевидно, мы можем потребовать инвариантности
расстояния от начала координат до заданной точки, то есть,
вокруг
начала координат. Очевидно, мы можем потребовать инвариантности
расстояния от начала координат до заданной точки, то есть,
![]() . Любое
преобразование, удовлетворяющее этому условию, можно записать в форме:
. Любое
преобразование, удовлетворяющее этому условию, можно записать в форме:
![]() -- некоторая величина, будем называть ее "углом поворота". Так же иногда
-- некоторая величина, будем называть ее "углом поворота". Так же иногда ![]() называют быстротой (N.B.!!!). Функции
называют быстротой (N.B.!!!). Функции ![]() и
и ![]() называются
гиперболическими косинусом и синусом
соответственно, причем
называются
гиперболическими косинусом и синусом
соответственно, причем
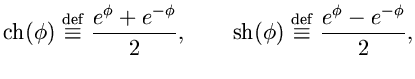
следовательно
![]() .
.
Доказательство универсальности подобной записи приводить не будем, ибо оно элементарно.
Пусть ![]() . Тогда
можем записать:
. Тогда
можем записать:
![]() .
.
![]() -- очевидно,
скорость движения начала координат системы со штрихом относительно
системы без штриха, то есть
-- очевидно,
скорость движения начала координат системы со штрихом относительно
системы без штриха, то есть ![]() . Перепишем:
. Перепишем:
![]() . Вот,
собственно, мы и получили вид преобразования. Осталось избавиться
от гиперболических функций (чисто для удобства). Введем обозначения:
. Вот,
собственно, мы и получили вид преобразования. Осталось избавиться
от гиперболических функций (чисто для удобства). Введем обозначения:
![]() ,
,
![]() . Тогда
значения гиперболического синуса и гиперболического косинуса можно
записать как:
. Тогда
значения гиперболического синуса и гиперболического косинуса можно
записать как:
![]() ,
,
![]() .
. ![]() будем
называть относительной скоростью, или просто скоростью.
будем
называть относительной скоростью, или просто скоростью.
Перепишем матрицу этого поворота:
Поворот вектора-столбца
![]() будем
записывать, как
будем
записывать, как
![]() (поворот
в плоскости
(поворот
в плоскости ![]() , то есть,
переход от системы отсчета
, то есть,
переход от системы отсчета ![]() , которая
движется относительно K с относительной скоростью
, которая
движется относительно K с относительной скоростью ![]() , ее оси
параллельны осям
, ее оси
параллельны осям ![]() , и движение
происходит параллельно оси
, и движение
происходит параллельно оси ![]() ). Эта
матрица поворота называется иногда матрицей Лоренца, и преобразования
координат-времени такого вида называется преобразованиями Лоренца.
Еще это преобразование иногда называют бустом.
). Эта
матрица поворота называется иногда матрицей Лоренца, и преобразования
координат-времени такого вида называется преобразованиями Лоренца.
Еще это преобразование иногда называют бустом.
1.3.5 Общепринятые обозначения
Общепринятые обозначения: 4х-вектор, метрический тензор, ковариантные и контрвариантные величины, немые индексы.
Для обозначения физических величин в пространстве Минковского удобно
использовать 4х-векторы. По определению, 4х-вектором является величина,
которая преобразуется при переходе из одной ИСО в другую в соответствии
с преобразованием Лоренца:
![]() . Очевидно,
мы можем получить из одного 4х-вектора другой 4х-вектор, домножая
его на инвариантную величину. Во всех остальных случаях справедливость
вывода 4х-вектора надо доказывать (см. вывод 4х-скорости). Компоненты
4х-вектора можно записывать в двух формах: ковариантной и контрвариантной.
Ковариантная величина пишется с индексом снизу (e.g.
. Очевидно,
мы можем получить из одного 4х-вектора другой 4х-вектор, домножая
его на инвариантную величину. Во всех остальных случаях справедливость
вывода 4х-вектора надо доказывать (см. вывод 4х-скорости). Компоненты
4х-вектора можно записывать в двух формах: ковариантной и контрвариантной.
Ковариантная величина пишется с индексом снизу (e.g. ![]() ), а контрвариантная
-- с индексом сверху (e.g $P^&mu#mu;). Ковариантная величина
получается из контрвариантной так:
), а контрвариантная
-- с индексом сверху (e.g $P^&mu#mu;). Ковариантная величина
получается из контрвариантной так: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . То есть,
квадрат длины четырехвектора мы можем записать как
. То есть,
квадрат длины четырехвектора мы можем записать как
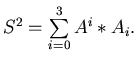
Вообще принято соглашение, по которому в подобных выражениях знак
суммы опускается, то есть
![]() , и говорится,
что индекс пробегает значения от 0 до 3, и подразумевается суммирование
по этому индексу. Если индексов 2, то подразумевается два суммирования.
Такая запись называется записью с немыми индексами. Для удобства
преобразования ко- и контрвариантных величин можно ввести так называемый
метрический тензор (метрику пространства Минковского), который имеет
вид:
, и говорится,
что индекс пробегает значения от 0 до 3, и подразумевается суммирование
по этому индексу. Если индексов 2, то подразумевается два суммирования.
Такая запись называется записью с немыми индексами. Для удобства
преобразования ко- и контрвариантных величин можно ввести так называемый
метрический тензор (метрику пространства Минковского), который имеет
вид:
Тогда преобразование ![]() в
в ![]() можно
записать как:
можно
записать как:
![]() .
.
Так же, скалярное произведение любых двух 4-векторов вводится как
Одно поднятие или опускание индекса при ![]() меняет
знак на противоположный.
меняет
знак на противоположный.
Все это кажется странной и ненужной заумью, однако, как в дальнейшем будет показано, использование метрического тензора и немых индексов очень сильно упрощает запись многих выражений.
1.3.6 Группа Лоренца, группа Пуанкаре
Введем понятие группы преобразований. Пусть есть два преобразования
![]() и
и ![]() .
.
![]() называется
группой, если для любых
называется
группой, если для любых ![]() и
и ![]() , таких,
что
, таких,
что ![]() ,
, ![]() , выполняются
следующие условия:
, выполняются
следующие условия:
- 1.
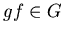 ,
, 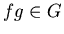
- 2.
-
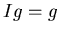 (
(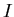 --
единичное преобразование,
--
единичное преобразование, 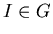 )
)
- 3.
-
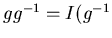 --
обратное преобразование.
--
обратное преобразование.
Очевидно, преобразования вида ![]() образуют
группу. Для любых преобразований группы Лоренца скалярное произведение
двух 4-векторов является инвариантом. Если
образуют
группу. Для любых преобразований группы Лоренца скалярное произведение
двух 4-векторов является инвариантом. Если ![]() и
и ![]() -- тензоры,
то инвариантом группы Лоренца будет
-- тензоры,
то инвариантом группы Лоренца будет
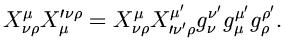
Так же инвариантом группы Лоренца является ранг тензора.
Еще одно очевидное свойство любого преобразования группы Лоренца:
![]() .
.
Возможны следующие частные случаи:
- 1.
-
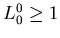 ;
;
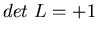 ; --
это преобразование группы Лоренца.
; --
это преобразование группы Лоренца.
- 2.
-
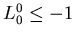 ;
;
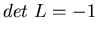 ,
,
и т.д. -- это преобразование группы Пуанкаре, то есть, преобразования с обращением времени и/или зеркальным отображением пространства.
2i.SU ©® 2015