4. Теория возмущения

Вопрос: В чем заключается теория возмущения?

Ответ: Теория возмущений позволяет исследовать сложную систему, если известна близкая к ней система, которая хорошо изучена (видимо потому, что она намного проще).

В широком смысле этого слова, теория возмущений есть совокупность методов разложения в ряд Тейлора по какому-нибудь малому параметру. Ряд Тейлора функции в окрестности точки есть:

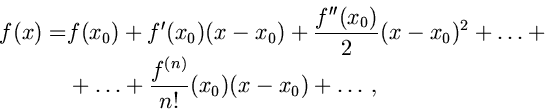
$\begin{displaymath} \begin{split}f(x)=&f(x_0) + f'(x_0)(x-x_0) + \frac{f''(x_0)}... ...&+ \ldots +\frac{f^{(n)}}{n!}(x_0)(x-x_0) + \ldots, \end{split}\end{displaymath}$

где -- первая производная в точке, --

вторая производная, $f^{(n)}$ --

n-ая производная функции в точке .

Разложение в ряд Тейлора позволяет находить значения функции в точке

если известно ее локальное поведение вблизи точки (т.е.известны значение функции в

и ее производные). Этот ряд есть разложение по параметру.

Если этот параметр мал (т.е. отклонение

от невелико), то каждый член ряда мал по сравнению с предыдущим, и для вычисления

можно ограничиться небольшим количеством членов ряда.

Пример: ряд Тейлора для функции вблизи точки имеет вид $sin(x) = x - \frac{x^3}{6} + \frac{x^5}{120} - \ldots$ . Вычислим с помощью этого ряда $sin(30) = sin(\pi/6) = 1/2$ . Нулевое приближение дает $sin(\pi/6)_{\text{пр}}= 0$ (функция взята в точке ). Это нас, естественно не удовлетворяет, нам нужна первая неисчезающая поправка к значению, равному нулю. В первом приближении, учитывая первое слагаемое ряда, имеем $sin(\frac{\pi}{6})_{\text{пр}}=\frac{\pi}{6} = 0.5236...$ , что уже гораздо лучше. Если же мы учтем второе кубическое слагаемое, то получим $sin(\frac{\pi}{6})_{\text{пр}}=\frac{\pi}{6}-\frac{(\pi/6)^3}{6}=0.4997...$ . Если велико, то ряд может сходиться медленно (и тогда от него мало пользы), а может и вообще расходиться. Т.е., теория возмущений работает, когда отклонение от известного значения (отклонение -- это и есть возмущение) невелико.

Конкретная схема теории возмущений сильно зависит от задачи, которую надо решать, и методы теории возмущений очень разнообразны.

Подробнее в книгах: Л.Д.Ландау, Е.М.Лифшиц "Механика", том 1 курса теоретической физики, М.: Наука, 1988, А.Найфэ, "Методы возмущений", М: Мир.

перейти к началу страницы