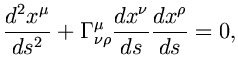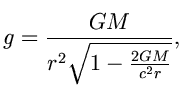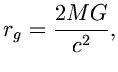2i.SU

Физика

Современные физические концепции

Следующий раздел: 2.2 Опыты подтверждающие общую теорию Выше по контексту: 2. Общая Теория Относительности Предыдущий раздел: 2. Общая Теория Относительности Алфавитный индекс

Разделы

2. Общая Теория Относительности

2.1 Общая теория относительности (Теория тяготения)

Вопрос: В чем заключается усложненный вариант теории относительности?

Ответ: Под усложненным вариантом, по видимому, подразумевается общая теория относительности (ОТО). Эйнштейн (A. Einstein), как известно, пытался построить общую теорию из которой бы следовали все взаимодействия, но не преуспел. Название ``Общая теория относительности'' принадлежит Эйнштейну. Это название является неадекватным и постепенно исчезает из литературы, заменяясь на ``теорию тяготения'' [1].

2.1.1 Основные идеи

Из школьного курса известны постулаты теории тяготения Ньютона. Теория Ньютона предполагает мгновенное распространение тяготения и уже по этому не может быть согласована со специальной теорией относительности, утверждающей что никакое взаимодействие не может распространяться со скоростью, превышающей в вакууме. Поэтому требовалась более общая теория тяготения (ею и стала ОТО). В линейном приближении (на относительно больших расстояниях и для относительно малых масс -- гравитационный потенциал мал $\vert\phi\vert\ll c^{2}$ ) ОТО переходит в теорию тяготения Ньютона.

Построение ОТО Эйнштейн начал в 1907 году и закончил вместе Х.Д. Гильбертом (H.D Hilbert) в 1915. Большой вклад в развитие математического аппарата теории внес в 1908-10 годах Г. Минковский (H. Minkowski).

В основе ОТО лежит экспериментальный факт равенства инертной массы (входящей во 2-ой закона Ньютона ) и гравитационной массы (входящей в закон тяготения) для любого тела. Это равенство проявляется в том, что движение тела в поле тяготения не зависит от его массы. Следствием этого является отсутствие гравитационно нейтральных тел .

В работе, сделанной в 1907 г., Эйнштейн предложил мысленный эксперимент [2]: представим себе гигантский небоскреб высотой 1000 км и физика, находящегося внутри свободно падающего лифта в этом небоскребе. Физик выпускает из рук платок и часы и убеждается, что они не падают на пол лифта. Если он сообщает этим вещам толчок, то они движутся равномерно и прямолинейно, пока не столкнутся со стенками лифта. Физик приходит к выводу: я нахожусь в ограниченной галилеевой системе. Условие ограниченности необходимо для того, чтобы можно было считать, что все тела испытывают одинаковое ускорение. Но физик, наблюдающий извне за падением лифта, будет судить о вещах совершенно иначе. Он видит, что лифт и все находящееся в нем движутся ускоренно в соответствии с законом тяготения Ньютона.

Этот пример показывает, что можно перейти от галилеевой системы к ускоренной, если учесть гравитационное поле. Иными словами гравитационное поле (в котором проявляется гравитационная масса) эквивалентно ускоренному движению (в котором проявляется инертная масса). Гравитационная масса и инертная масса характеризуют одно и то же свойство материи, рассматриваемое по-разному (разность массы современными экспериментальными методами не обнаружена). Таким образом, Эйнштейн пришел к принципу эквивалентности , который он так сформулировал в своей автобиографии:

В поле тяготения (малой пространственной протяженности) все происходит так, как в пространстве без тяготения, если в нем вместо ``инерциальной'' системы отсчета ввести систему, ускоренную относительно нее.

Данный принцип позволяет трактовать тяготение как искривление пространства-времени.

2.1.2 Уравнение движения в гравитационном поле

Тела в гравитационном поле движутся по геодезическим линиям, если на них не действуют другие (негравитационные) силы. Уравнение геодезической линии в искривленном пространстве-времени записывается в виде

$\displaystyle \frac{d^{2}x^{\mu}}{ds^{2}}+\Gamma ^{\mu}_{\nu \rho} \frac{dx^{\nu}}{ds}\frac{dx^{\rho}}{ds}=0,$

(5)

где -- координата, измеряемая вдоль геодезической линии, величины $\Gamma ^{\mu}_{\nu \rho}$ называются символами Кристофеля ( $\mu$ , $\nu$ , $\rho$ меняются от 0 до 3); $x^{\mu}$ , $x^{\nu}$ , $x^{\rho}$ -- компоненты четырехмерного вектора пространства-времени $(x^{0},x^{1},x^{2},x^{3})$ , где $(x^{1},x^{2},x^{3})=\vec{r}$ -- обычный трехмерный пространственный вектор, а $x^{0}=ct$ ( -- скорость света, -- время).

Искривление пространства-времени характеризуется символами Кристофеля. Если все символы Кристофеля равны 0, что соответствует отсутствию гравитационного поля, то уравнение геодезической переходит в уравнение прямой $\vec{a}=0$ , где $\vec{a}=\frac{d^{2}\vec{x}}{ds^{2}}$ -- ускорение тела, то есть мы получаем первый закон Ньютона . В приближении Ньютона геодезическими линиями являются прямые.

Подробно математический аппарат и выводы следствий общей теории относительности описаны в [4].

2.1.3 Черные дыры

Одним из интересных следствий общей теории относительности является существование черных дыр. Решение уравнений Эйнштейна (5), в пустоте, в случае изолированного сферически-симметричного источника поля массы называется решением Шварцшильда . В этом случае ускорение свободного падения имеет вид:

$\displaystyle g=\frac{GM}{r^{2}\sqrt{1-\frac{2GM}{c^{2}r}}},$

(6)

где

-- гравитационная постоянная,

-- скорость света,

-- расстояние до источника.

Это выражение отличается от Ньютоновского выражения для ускорения корнем в знаменателе. Величина стремится к бесконечности, когда стремится к

$\displaystyle r_{g}=\frac{2MG}{c^{2}},$

(7)

величина $r_{g}$ называется гравитационным радиусом (гравитационный радиус Солнца $r_{g\odot}\simeq 3$ км, гравитационный радиус Земли $r_{g\oplus}\simeq 0.9$ см). Сфера радиуса $r_{g}$ называется сферой Шварцшильда. Вторая космическая скорость в теории Ньютона дается выражением

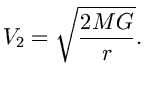$\displaystyle V_{2}=\sqrt{\frac{2MG}{r}}.$

(8)

Следовательно, при $r=r_{g}$ величина становится равной скорости света. Если сферическое тело массой сожмется до размеров, меньших , то свет не сможет выйти из под сферы Шварцшильда . Такие объекты получили названия черных дыр (термин "черная дыра" был введен в 1968 г. Дж. Уилером (J.A. Wheeler)).

Теоретическая астрофизика предсказывает возникновение черных дыр в конце эволюции массивных звезд; возможно существование черных дыр и другого происхождения (реликтовые черные дыры -- остатки после ``большого взрыва''). На данный момент астрономы наблюдают объекты, которые представляют из себя двойные звездные системы, в состав которых (как предполагается) входят черные дыры.

перейти к началу страницы