Пафнутий Львович Чебышев

Пафнутий Львович Чебышёв, один из крупнейших математиков прошлого века, родился в 1821 г. в Калужской губернии в имении отца. Первоначальное образование он получил дома. 16-ти лет Чебышёв был принят на физико-математический факультет Московского университета. Здесь он написал первую научную работу "Вычисление корней уравнения", за которую был награжден серебряной медалью.

В 1841 г. Чебышёв окончил Московский университет. Ему предстояло сделать выбор: либо идти на службу и бросить математику, либо целиком отдаться занятиям любимой наукой и терпеть лишения. Чебышёв выбрал последнее.

В 1846 г. он защитил магистерскую диссертацию "Опыт элементарного анализа теории вероятностей". В следующем году Чебышёв переехал в Петербург, где ему предложили должность адъюнкта в Петербургском университете. С 1860 г. он стал профессором того же университета. Много сил потратил Чебышёв на то, чтобы систематизировать и издать исследования Эйлера по теории чисел. Вопросы этой теории все более и более приковывали внимание самого Чебышёва. В 1849 г. он защитил докторскую диссертацию "Теория сравнений", посвященную теоретико-числовым проблемам. К этому же времени относятся знаменитые работы Чебышёва о простых числах.

Еще в глубокой древности ученых интересовал вопрос о том, по какому закону расположены в натуральном ряду простые числа: 2, 3, 5, 7, 11, 13, 17, 19, .... В "Началах" Евклида было доказано, что простых чисел бесконечно много. Хотя со времен Евклида прошло более двух тысяч лет, к его теореме ничего нового добавлено не было. Простые числа в натуральном ряду располагаются чрезвычайно прихотливо. С одной стороны, существуют простые числа-"двойники", которые отличаются одно от другого на 2, например: 3 и 5, 11 и 13, 17 и 19, 41 и 43 и т. д. Имеется гипотеза, что таких "двойников" бесконечно много. С другой стороны, если расположить все простые числа в ряд в порядке их возрастания:

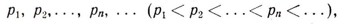
то можно всегда найти в этом ряду два соседних числа р_т и p_m+1, разность между которыми р_m+1- p_mкак угодно велика.

Рассмотрим теперь такую задачу. Пусть Пи(n) -число простых чисел, не превосходящих п. Мы не можем точно определить, каково будет Пи(n) для любого п; но нельзя ли его вычислить приближенно? Еще К. Гаусс и А. Лежандр, занимаясь этим вопросом, чисто эмпирически пришли к выводу, что Пи(n) для

больших п приближенно равно

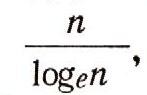
причем в знаменателе стоит натуральный логарифм, т. е. взятый по основанию е- 2,7182... . Но даже такие математики не смогли доказать замеченного ими факта. Только Чебышёву удалось сдвинуть проблему о простых числах с мертвой точки. Он показал, что если отношение

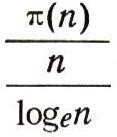
при п, неограниченно возрастающем, имеет предел, то этот предел равен единице. Впоследствии было показано, что этот предел существует. Это означает, что при больших п числитель Пи(n)примерно равен знаменателю n/log_eW .

Чебышёв доказал также так называемый "постулат Бертрана", выдвинутый французским математиком Ж. Бертраном, согласно которому между числами N и 2N - 2 при ,N>3 всегда содержится простое число. Исследования Чебышёва по теории чисел сразу же выдвинули молодого русского математика в число первых ученых Европы.

Второй цикл работ, прославивших Чебышёва, составили его исследования по теории вероятностей. Теория вероятностей - сравнительно молодая область математики. Первые задачи ее появились только в XVI-XVII вв. и были связаны с азартными играми (в кости, карты), а впоследствии с обработкой результатов наблюдений. И хотя многие ее основные предложения ко времени Чебышёва были уже хорошо известны, методы этой теории были лишены должной строгости, а приложения ее часто приводили к ошибочным результатам. Такие неудачи привели к разочарованию в теории вероятностей, некоторые говорили даже о "математическом скандале".

Только Чебышёв сумел вывести теорию вероятностей из кризиса. Он ввел и систематически рассматривал случайные величины, а также нашел новый метод доказательства теорем этой теории. С этого времени теория вероятностей стала полноправной математической дисциплиной.

Чебышёв является основателем русской школы теории вероятностей, которая занимает ведущее место в мировой науке. Благодаря работам Чебышёва и его школы теория вероятностей сделалась могучим орудием для исследования проблем физики (особенно квантовой механики), техники, биологии и других областей знания.

Еще в юности Чебышёв любил строить сложные механизмы. Эта любовь сохранилась у него на всю жизнь. Ученый изобрел более 40 типов шарнирных (или суставчатых, как он их называл) механизмов. Среди них была стопоходящая машина, воспроизводящая движения животных при ходьбе, гребной механизм, который повторял движение весел лодки, самокатное кресло и многие другие. Выставка этих механизмов, устроенная при жизни великого ученого в Чикаго, произвела потрясающее впечатление на современников. Чебышёв построил также арифмометр-полуавтомат, который хранится в Париже в Музее искусств и ремесел. Однако Чебышёв интересовался механизмами не только как изобретатель, но и как математик. Занимаясь теорией механизмов, он сумел увидеть в ней новые математические проблемы, которые в его время были еще совершенно не изучены. Его работы, посвященные этим проблемам, положили начало теории наилучшего приближения функций. Эта теория с тех пор успешно развивается.

У П. Л. Чебышёва было много учеников. Он по праву считается основателем петербургской математической школы, которая насчитывает в своих рядах таких первоклассных ученых, как Е. И. Золотарев, А. А. Марков, А. М. Ляпунов, Г. Ф. Вороной.

Заслуги П. Л. Чебышёва были признаны всем ученым миром. В 38 лет он был избран членом Петербургской академии наук, затем членом Парижской и Берлинской академий, Лондонского королевского общества и многих других академий.

Ученый прожил долгую жизнь и до последней минуты много и плодотворно работал. Умер Чебышёв в 1894 г. За письменным столом он внезапно почувствовал себя плохо и вскоре скончался от паралича сердца.

перейти к началу страницы