Математика

Содержание раздела

Выдающиеся математики

Леонард Эйлер

Этот крупнейший математик XVIII столетия родился в швейцарском городе Базеле в 1707 г. Отец его был пастором и хотел, чтобы сын тоже стал священником. В Базельском университете Леонард Эйлер штудировал богословие и древние языки, но слушал также лекции по математике профессора Иоганна Бернулли, знаменитого ученого, принадлежавшего к научной школе Лейбница.

Заметив блестящие способности своего слушателя, Бернулли стал с ним заниматься дополнительно. Вскоре математика одержала верх над богословием, и жизненное призвание Леонарда определилось окончательно. В 1727 г. Эйлер по приглашению Петербургской академии наук приехал в Россию. Ему было 20 лет.

В Петербурге Эйлер попал в круг выдающихся ученых - математиков, физиков, астрономов, получил широкие возможности для издания трудов, полное материальное обеспечение. Он с увлечением принялся за работу, и в "Записках" академии стали появляться его статьи, привлекшие внимание ученых всей Европы. А вскоре он становится, по единодушному признанию современников, первым математиком мира.

Деятельность Эйлера в Петербурге не ограничилась теоретическими исследованиями в математике. В течение нескольких лет он работает в географическом отделе академии над усовершенствованием карт России. Он готовит большой двухтомный труд по теории кораблестроения и кораблевождения и одновременно публикует книгу по теории музыки. Ученый ведет занятия со студентами университета при академии и пишет учебник арифметики для школьников. Он неоднократно участвует в различных комиссиях по техническим вопросам. Отдавая всю свою кипучую энергию академии, Эйлер открыто признавал, что всем, чем стал, он обязан прежде всего пребыванию в ней.

Неустойчивое и тревожное положение, создавшееся в России во время регентства Анны Леопольдовны, заставило Эйлера в 1741 г. перейти на работу в Берлинскую академию наук. При этом он сохранил самые тесные связи с Россией. Эйлер регулярно печатает в изданиях Петербургской академии примерно половину своих статей, редактирует математический отдел ее ученых записок, сообщает в своих частых письмах научные новости и т. д. Годами в берлинском доме Эйлера жили молодые русские ученые, с которыми он вел занятия.

Положение дел в Берлинской академии наук во многом не удовлетворяло Эйлера, и в 1766 г. он вернулся в Петербург.

Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Опираясь на свои изумительные способности, он продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже не писал сам, а диктовал ученикам, которые проводили за него и наиболее громоздкие вычисления. О работоспособности Эйлера на склоне лет говорит такой феноменальный факт: за 1777 г. он с секретарем подготовил около 100 научных статей, т. е. почти по две статьи в неделю! Этот неустанный творческий труд оборвался лишь смертью Эйлера в 1783 г.

Творчество Эйлера поражает исключительной продуктивностью. Он оставил более 800 трудов, причем многие из них - большие книги в двух-трех томах. При жизни Эйлера статьи его не успевали печатать. Шутя он говорил, что оставит для академического журнала работ на 20 лет. Великий математик был превосходным вычислителем, но на этот раз он ошибся: посмертно печатали его неизданные сочинения еще около 80 лет!

Эйлер был не только самым плодовитым математиком всех времен. Он был необыкновенно разносторонним ученым, занимался всеми вопросами современной ему математики и ее приложений, а некоторые отделы начал разрабатывать впервые. Теория чисел и теория движения Луны, геометрия и оптические приборы, алгебра и сопротивление материалов, тригонометрия и баллистика - все это и многое другое интересовало его.

Человечество обязано Эйлеру многими ценными изобретениями, усовершенствованиями и техническими теориями. Он заложил основы современной техники изготовления ахроматических зрительных приборов, которые дают изображения, свободные от искажающего рассеяния цветов благодаря подбору линз с различными показателями преломления. Он создал первую теорию расчета действия турбин. Заложил основы теории гироскопа-волчка, которая играет очень большую роль в современной технике. Но, как ни велики эти заслуги Эйлера, главным в его жизни была разработка проблем математики. Ей он посвятил около 315 сочинений.

Около 150 работ Эйлера - статьи и книги по теории чисел. Значение их точно выразил великий русский математик П. Л. Чебышёв, продолживший многие исследования Эйлера: "Эти изыскания требовали новых приемов, открытия новых начал, одним словом, основания новой науки. Это было сделано Эйлером".

В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в большую и важную науку - топологию, которая изучает общие свойства пространства и фигур. Приведем два замечательных открытия Эйлера, относящихся к топологии.

Первое из них - решение задачи о мостах. Река образует острова, и через два речных рукава перекинуто 7 мостов. Спрашивается: можно ли пройти все 7 мостов так, чтобы каждый был пройден по одному лишь разу? Эйлер показал, что это невозможно, и рассмотрел более общую задачу, в которой речь идет о любом числе местностей, как-либо разделенных рукавами рек и соединенных мостами. Задачу о мостах часто формулируют несколько по-иному, спрашивая, можно ли описать фигуру, составленную из отрезков прямых или дуг кривых, так, чтобы каждое звено было пройдено один, и только один, раз.

Другое открытие представляет важную теорему учения о многогранниках: Эйлер установил и доказал, что числа вершин В, ребер Р и граней Г всякого многогранника, в котором нет "дыр", связаны формулой: В + Г = Р + 2.

Главной областью математических работ Эйлера был математический анализ, т. е. дифференциальное и интегральное исчисления и ряд других примыкающих к ним наук. Здесь невозможно даже вкратце перечислить открытия Эйлера в этой области. Упомянем только, что он открыл удивительную зависимость между тригонометрическими функциями (синусом и косинусом) и показательной функцией е^х:

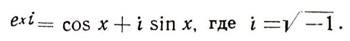
Вместе с тем Эйлер впервые разработал общее учение о логарифмической функции, согласно которому все комплексные числа, кроме нуля, имеют логарифмы, причем каждому числу соответствует бесчисленное множество значений логарифма.

Знаменитый французский ученый П. Лаплас говорил: "Читайте, читайте Эйлера, он наш общий учитель". Действительно, по математическим руководствам Эйлера "Введение в анализ", "Дифференциальное исчисление", "Интегральное исчисление", "Универсальная арифметика" (т. е. алгебра), по его книгам по механике и физике училось несколько поколений. Главное содержание этих книг вошло и в современные учебники.

Все сочинения Эйлера написаны очень доступно и увлекательно. Юный любитель математики может с пользой и интересом прочитать, конечно, с карандашом в руке первую часть "Введения в анализ". Она читается не так быстро, как приключенческий роман, но с не меньшим увлечением.

перейти к началу страницы