Готфрид Вильгельм Лейбниц

Готфрид Вильгельм Лейбниц родился в Германии в г. Лейпциге в 1646 г. Любознательный мальчик уже с 6 лет вел интересные беседы по истории со своим отцом - профессором Лейпцигского университета. К 12 годам он хорошо изучил латинский язык и увлекся древнегреческим. Особенно его интересовали древние философы, и он мог подолгу размышлять о философских теориях Аристотеля или Демокрита. В 15 лет Лейбниц поступает в Лейпцигский университет, где усердно изучает право и философию. Он очень много читает, среди его любимых книг -книги Р. Декарта, Г. Галилея, И. Кеплера и Т. Кам-панеллы. Свои колоссальные знания по математике Лейбниц приобрел, будучи в этой области знаний самоучкой. Через три года, окончив университет, он покинул Лейпциг. Существует предание, что он был обижен отказом ученого совета университета присвоить ему степень доктора прав. Отказ объяснили тем, что Лейбниц был... слишком молод!

Началась жизнь, полная напряженного труда и многочисленных путешествий. Легко себе представить, как неудобно было путешествовать в неуклюжих каретах по тряским дорогам Европы тех времен. Лейбниц умел не терять времени даром - много удачных мыслей пришло ему в голову именно во время этих продолжительных поездок. Лейбниц отличался исключительной способностью быстро "входить" в задачу и решать ее наиболее общим способом. Однако интересных идей приходило в голову Лейбницу больше, чем он успевал их записывать. Чувствуя, что все это богатство мыслей ему не успеть переработать в ясные и завершенные теории, Лейбниц часто ограничивался сообщением только сути дела. Такая "охота" за идеями была по душе Лейбницу. Он шутливо сравнивал себя с тигром, о котором рассказывают, что если этот зверь не схватит чего-либо в первый, второй или третий прыжок, то предоставляет добыче убежать.

Люди, лично знавшие Лейбница, писали о нем как о мягком и отзывчивом человеке, очень скромном в своих привычках. Лейбниц был дипломатом, надворным советником, воспитателем княжеских детей, историографом. Почти все время он работал при дворах немецких государей, князей и герцогов. Но он всегда помнил о своей любимой науке. Он умел извлекать много полезного из любого дела, любого знакомства. Лейбниц хорошо понимал, что для успешного развития науки необходимы специальные научные общества, академии, в которых ученые могли бы свободно обмениваться мнениями. По предложению Лейбница в 1700 г. основывается Берлинская академия наук, в которой ему предоставляют почетное место первого президента. Он хлопочет о создании академий в других городах Европы и даже всеевропейской академии наук. Неоднократные беседы Лейбница с Петром I о развитии наук в России имели большое значение для организации Петербургской академии наук. Петр I в знак признания заслуг Лейбница сделал его тайным советником.

Удивительный ум Лейбница породил большое количество плодотворных идей почти во всех областях человеческих знаний. В физике Лейбниц сформулировал основной закон сохранения кинетической энергии, или, как он ее называл, "живой силы": mv²/2 .

Стараниями Лейбница был положен конец путанице с календарями в Германии и был принят григорианский календарь. Размышляя над философскими и математическими вопросами, Лейбниц решил, что самым надежным средством искать и находить истину может стать математика. Всю свою сознательную жизнь он стремился выразить законы мышления, человеческую способность думать в виде математического исчисления. Для этого необходимо, учил Лейбниц, уметь обозначать любые понятия или идеи определенными символами, комбинируя их в особые формулы, и сводить правила мышления к правилам вычислений по этим символическим формулам. Заменяя обычные слова четко определенными символами, Лейбниц стремился избавить наши рассуждения от всякой неопределенности и возможности ошибиться самому или вводить в заблуждение других. Если, мечтал Лейбниц, между людьми возникнут разногласия, то решаться они будут не в длинных и утомительных спорах, а так, как решаются задачи или доказываются теоремы. Спорщики возьмут в руки перья и, сказав: "Начнем вычислять!", примутся за расчеты.

Лейбниц одновременно с Ньютоном и независимо от него открыл основные принципы дифференциального и интегрального исчислений. Теория приобрела свою силу после того, как Лейбницем и Ньютоном было доказано, что дифференцирование и интегрирование - взаимно обратные операции. Лейбниц увидел здесь ту замечательную возможность, которую открывает применение символического метода.

Любой человек, изучив небольшое число правил действий с символами, обозначающими операции дифференцирования и интегрирования, становится обладателем мощного математического метода. В наше время такие символы операций называют операторами. Операторы дифференцирования d ( ) и интегрирования интеграл ( ) dx действуют на функции, "перерабатывая" их в другие, точно вычисляемые функции (см. ст. "Интеграл и производная"). Лейбниц разрабатывает особую алгебру действий с этими операторами. Он доказывает, что обычное число а можно выносить за знак оператора:

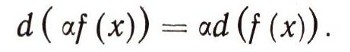
или

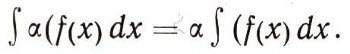
Одинаковые операторы можно выносить за скобку:

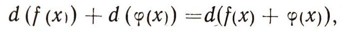
или

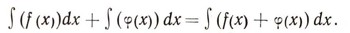
Сокращенно эти свойства можно выразить соотношением :

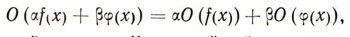
где а и бета - числа, О - линейный оператор. Многократное применение операторов можно понимать как степень оператора, например, для d ( ):

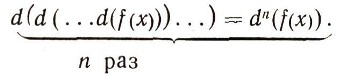
То, что основные операторы математического анализа являются взаимно обратными, Лейбниц подчеркивает своей символикой, утверждая, что d ( ) и

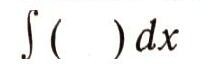
так же взаимно обратны, как степени и корни в обыкновенном исчислении. Употребляют также обозначение, аналогичное обозначению а^1-числа, обратного а, причем произведение а * а^-1 =1. Обозначая операторы

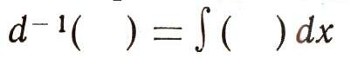
или, на-

оборот,

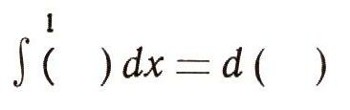
и понимая под их произведением последовательное их применение, имеем:

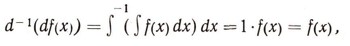
т. е. такое произведение есть "единица", не меняющая функцию.

Анализируя правила логики, правила рассуждений, Лейбниц увидел, что и здесь можно применить подходящую символику и свести разнообразные приемы умозаключений к небольшому числу точно определенных операций. Такое исчисление умозаключений, или, как его теперь называют, алгебра логики, в наши дни приобрело большое значение. На его основе создаются современные электронные вычислительные машины; теория таких "думающих" автоматов имеет большое принципиальное значение.

Всю Вселенную Лейбниц рассматривал как гигантский самоорганизующийся автомат. Отмечая роль, которую сыграли идеи Лейбница для кибернетики, творец кибернетики Н. Винер в шутку писал: "Если бы мне пришлось выбирать в анналах истории наук святого - покровителя кибернетики, то я выбрал бы Лейбница".

Сам Лейбниц также стремился воплотить в машине свои мысли о механизации и автоматизации мыслительных процессов. Он построил металлическую счетную машину, которая могла складывать, вычитать, умножать целые числа. Эта счетная машина произвела большое впечатление на ученых того времени. После того как Лейбниц показал свою машину в Лондонском королевском обществе (так называется английская академия наук), его избрали членом этого общества.

Поиски операторов и исчислений в области систем алгебраических уравнений первой степени со многими неизвестными привели Лейбница к созданию важного понятия определителя системы таких уравнений. В наши дни определитель стал совершенно необходимым инструментом как в самой математике, так и в разнообразнейших ее применениях.

Необыкновенная проницательность Лейбница сказывается и в его отношении к математическим играм. Лейбниц пишет: "...игры, как требующие ловкости, так и основанные на случайности, дают громадный материал для научных занятий". Слова ученого оказались пророческими - современная математическая теория игр имеет огромное значение не только для математики, но и для экономики, военного дела и многих других областей человеческой деятельности.

Смысл всей своей жизни Лейбниц видел в умственном творчестве, в создании общедоступных идей, полезных человеку в познании природы. Надо сказать, что он был честолюбив и очень чувствителен к признанию своих действительно больших заслуг перед наукой. Тем больнее был для него спор с И. Ньютоном о приоритете создания математического анализа. И совсем тяжелыми были последние годы жизни, когда старый и больной Лейбниц умирал забытый всеми. Только необычайная воля к труду и, как всегда, ясность мысли скрашивали его одиночество. Он умер в 1716 г. Смерть его не была отмечена ни в Берлинской академии наук, ни в Лондонском королевском обществе. Биограф Лейбница пишет, что он был похоронен как нищий, а не как выдающийся гений Германии. Только спустя много лет ему в родном городе был поставлен памятник. Но истинным памятником Лейбницу являются его математические идеи, которые и в наши дни продолжают приносить чудесные плоды на благо человека.

перейти к началу страницы