Франсуа Виет

Трудно перечислить всех ученых, открытия которых изучаются в современной "школьной" математике. Но есть два математика, которые сделали для нее больше других: это геометр Древней Греции Евклид и "отец современной алгебры" Франсуа Виет.

Франсуа Виет родился во Франции в 1540 г. в городке Фонтеней. Адвокат по профессии, он был всесторонне образованным человеком, хорошо знал древние языки, астрономию. Но его истинным призванием была математика. Увлеченный математической задачей, он мог работать над ней долгое время без еды и сна. Виет умел активно применять свои способности и знания к всевозможным трудным задачам не только из алгебры и геометрии. Известно, например, что он любил разгадывать зашифрованные письма. Во время войны Франции с Испанией вся тайная переписка испанцев свободно читалась французами, так как Виет всякий раз разгадывал испанский шифр, как бы его ни запутыв'али вражеские шифровальщики. Не представляя себе могущества человеческого ума, испанцы думали, что французам помогает дьявол. Они даже жаловались римскому папе и просили его уничтожить эту "дьявольскую силу".

Виета называют творцом современной алгебры за очень важное нововведение - он целеустремленно и последовательно применял в алгебре буквенное исчисление. Чтобы отчетливее представить себе, в чем суть буквенного исчисления Виета и почему оно так важно для всей современной алгебры, посмотрим, что представляла собой алгебра до него. Почти все действия и знаки записывались словами, не было и намека на те удобные, почти автоматические правила, которыми сейчас умеет пользоваться каждый ученик. Поэтому нельзя было записывать и, следовательно, изучать в общем виде алгебраические уравнения или какие-нибудь другие алгебраические выражения. Необходимо было доказать, что существуют такие общие действия над всеми числами, которые от этих самых чисел не зависят.

Виет и его последователи установили, что не имеет значения, будет ли рассматриваемое число количеством предметов или длиной перпендикуляра. Главное, что с этими числами можно производить алгебраические действия и в результате снова получать числа того же рода. Не имеет значения также, известно ли нам число или неизвестно. А если нам не важны цифровая запись или геометрическое истолкование каждого рассматриваемого числа, то все числа как бы однородны и их можно обозначать какими-нибудь отвлеченными знаками, например буквами латинского алфавита. Виет не только ввел свое буквенное исчисление, но сделал принципиально новое открытие, поставив перед собой цель изучать не числа, а действия над ними. Это была удачная мысль, и она стала сразу приносить обильные плоды. Например, вскоре был доказан общий алгебраический закон умножения: умножение отрезков есть та же операция, что и умножение чисел. Появилась возможность записывать алгебраические выражения в виде формул.

Однако у самого Виета алгебраические обозначения, или, как сейчас говорят, алгебраические символы, были мало похожи на наши. Сравните современную запись кубического уравнения:

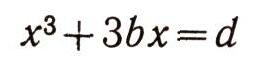
и запись этого же уравнения в обозначениях Виета: A cubus + B planum in A 3 aequatur D solido. Как видите, здесь еще очень много слов, но ясно, что эти слова уже играют роль наших символов; так, латинское слово cubus после неизвестного А (неизвестное обозначалось гласной буквой) означает наше "в кубе". Слово aequatur (в переводе на русский -"равный") написано вместо нашего знака " = ", умножение чисел В и А обозначено предлогом in (все, что осталось после сокращения от выражения "взять во столько-то раз больше"). Остальные слова - это следы прошлого, следы того, что и у Виета алгебра еще не полностью освободилась от посторонних для нее влияний геометрии.

Но уже и такой способ записи позволил Виету сделать важные открытия при изучении общих свойств алгебраических уравнений. Особенно гордился Виет всем известной теперь теоремой его имени о выражении коэффициентов уравнения через его корни, хотя под корнями он понимал только положительные числа, не признавал за корни отрицательные и совсем не подозревал о существовании комплексных чисел. При составлении обширных таблиц тригонометрических функций Виет с большим искусством применил десятичные дроби. Глубокий интерес к тригонометрии у него был вызван желанием сделать астрономию более точной. Увлекшись тригонометрией, Виет и здесь получает значительные результаты. Например, он выводит выражения для синусов и косинусов кратных дуг через sin x и cos X при помощи формул, которые мы теперь записали бы в виде:

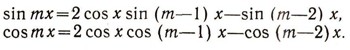
Эти знания из тригонометрии Виет с успехом применял как в алгебре, так и в геометрии. Используя представление о круге как о пределе вписанных в него многоугольников при увеличении числа их сторон, Виет вычислил число Пи до 18-го знака после запятой (из них 11 знаков верны).

Умение решать алгебраические задачи при помощи геометрии и тригонометрии принесло Виету славу победителя турнира лучших математиков того времени. Голландский математик Адриан ван-Роумен предложил математикам всего мира решить уравнение 45-й степени с числовыми коэффициентами. Французским математикам он не послал свой вызов, как бы намекая на то, что во Франции нет математиков, способных справиться с этой задачей. Узнав об этом, король Франции Генрих IV, на службе у которого в то время состоял Виет, воскликнул: "И все же у меня есть математик, и весьма выдающийся. Позовите Виета!" И действительно, Виет тут же, в присутствии короля, нашел один корень предложенного уравнения, а на следующий день нашел еще 22 его положительных корня. После этого ван-Роумен стал ревностным почитателем Виета.

Виет решил при помощи циркуля и линейки знаменитую задачу, сформулированную геометром Древней Греции Аполлонием из Перги. По условию этой задачи надо построить круг, касательный к трем данным кругам. Гордясь найденным решением, Виет называл себя "Аполлонием из Галлии" (Галлией в старину называли Францию).

В последние годы своей жизни Виет занимал важные посты при дворе короля Франции. Умер Виет в Париже в 1603 г.

Бурно развивающаяся математика наших дней, конечно, использует идеи и методы, во много раз превосходящие по глубине и общности идеи и методы, которые разработал Виет. Но и сейчас для нас интересна и ценна острая алгебраическая мысль Виета, который широко распахнул перед математикой двери в новый мир современной алгебры. Не будем забывать, что в ее основе лежит буквенное исчисление Франсуа Виета.

перейти к началу страницы