Архимед

Великий математик, механик и инженер древности Архимед родился в 287 г. до н. э. (предположительно) в Сиракузах - богатом торговом городе Сицилии. Отцом его был астроном Фидий, который привил сыну с детства любовь к математике, механике и астрономии. В Александрии Египетской - научном и культурном центре того времени - Архимед познакомился со знаменитыми александрийскими учеными: астрономом Кононом, разносторонним ученым Эратосфеном, с которыми потом переписывался до конца жизни. В то время Александрия славилась своей библиотекой, в которой было собрано более 700 тыс. рукописей. По-видимому, именно здесь Архимед познакомился с трудами Демокрита, Евдокса и других замечательных греческих геометров, о которых он упоминал в своих сочинениях.

Уже при жизни Архимеда вокруг его имени создавались легенды, поводом для которых служили его поразительные изобретения, производившие ошеломляющее действие на современников. Известен рассказ о том, как Архимед сумел определить, сделана ли корона царя Гиерона из чистого золота или ювелир подмешал туда значительное количество серебра. Удельный вес золота был известен, но трудность состояла в том, чтобы точно определить объем короны: ведь она имела неправильную форму! Архимед все время размышлял над этой задачей. Как-то он принимал ванну, и тут ему пришла в голову блестящая идея: погружая корону в воду, можно определить ее объем, измерив объем вытесненной ею воды. Согласно легенде, Архимед выскочил голый на улицу с криком "Эврика!", т. е. "Нашел!". И действительно, в этот момент был открыт основной закон гидростатики.

Другая легенда рассказывает, что построенный Гиероном в подарок египетскому царю Птолемею роскошный корабль "Сирокосия" никак не удавалось спустить на воду. Архимед соорудил систему блоков (полиспаст), с помощью которой он смог проделать эту работу одним движением руки. Этот случай или размышления Архимеда над принципом рычага послужили поводом для его крылатых слов: "Дайте мне точку опоры, и я сдвину Землю".

Архимед прославился и другими механическими конструкциями. Изобретенный им бесконечный, или архимедов, винт для вычерпывания воды до сих пор применяется в Египте. Архимед построил планетарий, или "небесную сферу", при движении которой можно было наблюдать движение пяти планет, восход Солнца и Луны, фазы и затмения Луны, исчезновение обоих тел за линией горизонта.

Инженерный гений Архимеда с особой силой проявился во время осады Сиракуз римлянами в 212 г. А ведь в это время ему было уже 75 лет! Построенные Архимедом мощные метательные машины забрасывали римские войска тяжелыми камнями. Думая, что они будут в безопасности у самых стен города, римляне кинулись туда, но в это время легкие метательные машины близкого действия забросали их градом ядер. Мощные краны захватывали железными крюками корабли, приподнимали их кверху, а затем бросали вниз, так что корабли переворачивались и тонули.

Римляне вынуждены были отказаться от мысли взять город штурмом и перешли к осаде. Знаменитый историк древности Полибий писал: "Такова чудесная сила одного человека, одного дарования, умело направленного на какое-либо дело... римляне могли бы быстро овладеть городом, если бы кто-либо изъял из среды сиракузян одного старца". Только вследствие измены Сиракузы были взяты римлянами осенью 212 г. При этом Архимед был убит. Плутарх сохранил нам яркий рассказ о его смерти: "К Архимеду подошел солдат с мечом в руке, чтобы убить его. Но Архимед настойчиво просил его подождать одну минуту, чтобы задача, которой он занимался, не осталась нерешенной; солдат, которому не было дела до его доказательства, пронзил его своим мечом".

Архимед был замечательным механиком-практиком и теоретиком, но основным делом его жизни была математика. По словам Плутарха, Архимед был просто одержим ею. Он забывал о пище, совершенно не заботился о себе. Его работы относились почти ко всем областям математики того времени: ему принадлежат замечательные исследования по геометрии, арифметике, алгебре. Так, он нашел всё полуправильные многогранники, которые теперь носят его имя (см. рис. на стр. 279), значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений вида х²(а±х) = b, корни которых он находил с помощью пересечения параболы и гиперболы. Архимед провел и полное исследование этих уравнений, т. е. нашел, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать. Остались отрывки работы Архимеда, в которой он развивает математическую теорию популярной в Греции игры (так называемой стомахии), предвосхищая, таким образом, более чем на 2 тыс. лет создание математической теории игр. Но главное его внимание было сосредоточено на трех типах проблем:

1. Определение площадей криволинейных фигур или, соответственно, объемов тел. Вы уже знаете, наверное, как определять площади прямолинейных фигур, площадь круга, объем призмы, пирамиды, цилиндра и конуса. Все это умели делать греки и до Архимеда. Но только он нашел общий метод, позволяющий найти любую площадь или объем. Трудно переоценить значение этого метода, без которого была бы немыслима ни физика, ни астрономия. Идеи Архимеда легли в основу интегрального исчисления.

Сам Архимед определил с помощью своего метода площади и объемы почти всех тел, которые рассматривались в античной математике. Лучшим своим достижением он считал определение поверхности и объема шара. Он просил выбить на своей могиле шар, вписанный в цилиндр.

2. Пусть дана некоторая кривая линия. Как определить касательную в любой ее точке? Или, если переложить эту проблему на язык физики, пусть нам известен путь некоторого тела в каждый момент времени. Как определить скорость его в любой точке? В школе учат, как проводить касательную к окружности. Древние греки умели, кроме того, находить касательные к эллипсу, гиперболе и параболе. Первый общий метод решения и этой задачи был найден Архимедом. Этот метод впоследствии лег в основу дифференциального исчисления.

3. В математике, физике и астрономии очень важно уметь находить наибольшие и наименьшие значения изменяющихся величин - их экстремумы. Например, как среди цилиндров, вписанных в шар, найти цилиндр, имеющий наибольший объем? Все такие задачи в настоящее время могут быть решены с помощью дифференциального исчисления. Архимед первым увидел связь этих задач с проблемами опреде-

ления касательных и показал, как с их помощью можно решать задачи на экстремумы.

Огромное значение для развития математики имело вычисленное Архимедом отношение длины окружности к диаметру C/D, т. е. число и, с большой степенью точности. Для этого он рассматривал последовательность вписанных и описанных правильных многоугольников с числом сторон 6, 12, 24, 48 и 96 и нашел отношения их периметров к диаметру! Ясно, что

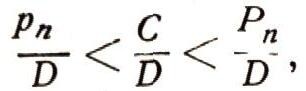
где р_п - периметр вписанного, а Р_п - описанного n-угольника. Архимед нашел, что

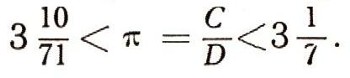
Идеи Архимеда почти на два тысячелетия опередили свое время. Только в XVII в. ученые смогли продолжить и развить труды великого греческого математика. Только тогда было раскрыто их подлинное значение. Лейбниц, один из творцов дифференциального и интегрального исчислений, писал: "Внимательно читая сочинения Архимеда, перестаешь удивляться всем новейшим открытиям геометров".

перейти к началу страницы