Решение игры в смешанных стратегиях. Основная теорема теории игр

Мы знаем, что если нижняя цена игры а. равна верхней бета (максимин равен минимаксу), то игра имеет седловую точку и по крайней мере одно решение в чистых стратегиях.

А если а не равно бета? Можно доказать, что и в этом случае решение всегда есть, только оно лежит не в области чистых, а в области смешанных стратегий. Решением игры называется такая пара стратегий -в общем случае смешанных, систематическое применение которых обеспечивает каждой стороне максимально возможный для нее по условиям игры выигрыш, определяемый ценой игры. Если же одна из сторон отступает от своей оптимальной стратегии (в то время как другая продолжает придерживаться своей), то это ни в коем случае не может быть выгодно для отступающего: это либо оставит его выигрыш неизменным, либо уменьшит. Доказано, что каждая конечная игра имеет решение (возможно, в области смешанных стратегий). Это положение называется основной теоремой теории игр.

Введем специальное обозначение для смешанных стратегий. Пусть К, применяет свои стратегии K₁ К₂, К₃с частотами соответственно p₁ р₂, р₃(р₁+ р₂ + р₃ = 1). Эту смешанную стратегию будем обозначать:

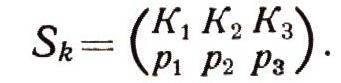
Аналогично смешанную стратегию игрока С будем обозначать:

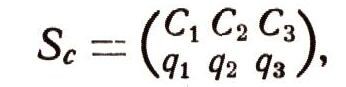
где q₁ + q₂ + q₃ = 1.

Очевидно, любая чистая стратегия - частный случай смешанной, в которой все частоты, кроме одной, равны нулю, а одна - единице. Решение игры - пару оптимальных стратегий -будем обозначать S_k^* и S_c^* , а соответствующий выигрыш (цену игры) v. Очевидно, что цена игры У не может быть меньше нижней и больше верхней цены:

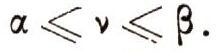
В первом примере мы путем нестрогих соображений догадались, что решение игры должно быть:

а цена игры v = 0. Проверим это. Пусть мы ("красные") держимся своей стратегии S_k^* , т. е. ищем С в убежищах I и II одинаково часто, чередуя эти стратегии случайным образом. Может ли С улучшить свое положение (повысить свой выигрыш), отступая любым образом от своей стратегии S_c^* ? Очевидно, нет. А если одностороннее отступление от стратегии S_k^* придет в голову нам (в то время как разумный С будет держаться стратегии S_c^* ), то это нам тоже не может быть выгодно. Значит, мы и в самом деле нашли решение игры и ее цену v = 0. Правда, эта игра была довольно простой! Уже второй пример дает игру, решение которой не так очевидно. Из того, что в нем а не равно бета, следует только, что решение нужно искать в смешанных стратегиях.

Но каково это решение? Какова цена игры? Выгодна ли игра "красным", или "синим", или никому из них? Ответы на эти вопросы вы можете найти в книге автора данной статьи, указанной в библиографическом указателе "Что читать по математике".

перейти к началу страницы