Некоторые современные направления развития теории вероятностей

Основные понятия современной теории вероятностей - понятия случайного процесса, случайного поля, информации. Физика, химика, биолога и техника интересует в первую очередь изучение процессов, т. е. явлений, протекающих во времени. Так, при изучении химической реакции или же в технологических процессах на химическом предприятии нас всегда интересует, как при заданных условиях эта реакция протекает во времени, какая часть вещества уже вступила в реакцию, когда практически реакция уже закончилась.

Представим себе, что мы задались целью проследить за движением какой-либо молекулы газа или жидкости. В случайные моменты времени эта молекула сталкивается с другими молекулами, меняет при этом свою скорость и направление движения. Ряд физических задач требует для своего решения умения вычислять вероятности того, как много молекул успеет за тот или иной промежуток времени передвинуться на то или иное расстояние. Так, например, если приведены в соприкосновение две жидкости, то начинается взаимное проникновение молекул одной жидкости в другую - происходит диффузия. Как быстро протекает процесс диффузии, по каким законам, когда образующаяся смесь газов становится практически однородной? На все эти вопросы дает ответ статистическая теория диффузии, в основе которой лежат вероятностные расчеты.

Весьма важный круг явлений происходит по принципу радиоактивного распада. Это явление, как известно, состоит в том, что в случайные моменты времени какие-то атомы радиоактивного вещества распадаются, превращаясь в атомы другого вещества. Каждый распад происходит подобно взрыву, с выделением некоторой энергии. Если масса распадающегося вещества не слишком велика (меньше определенной величины, называемой критической), то распады атомов, как показывают многочисленные наблюдения, происходят независимо друг от друга. Для изучения процесса радиоактивного распада весьма важно определить вероятность того, что за определенный промежуток времени распадается то или иное число атомов. Впрочем, в точности такая задача возникает в телефонном деле, при проектировании пропускной способности мостов, в теории надежности, в экономике, в военном деле, в технике. Независимо от конкретного воплощения вопрос, который постоянно возникает, ставится так: как велика вероятность того, что за определенный промежуток времени наступит некоторое число определенных событий (вызовов абонентов на телефонную станцию; машин, которым требуется пересечь мост; отказов элементов, из которых составлено сложное оборудование, и т. д.)? При весьма широких условиях искомая вероятность может быть вычислена по формуле:

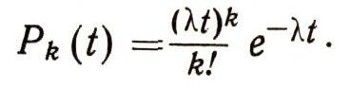
Здесь P_k(t) означает вероятность того, что за промежуток времени t произойдет ровно k событий; Я - постоянная, так называемая интенсивность наступления событий, е = 2,71828..., k! = 1*2*3 ..... k.

В начале статьи была приведена табличка приходов судов в Одесский порт. Нижняя строка ее вычислялась как раз по этой формуле. Эта же формула широко используется в физике для подсчета числа космических частиц, попадающих на определенный участок земной поверхности за время t. Она же служит для вычисления числа ламп в электронной вычислительной машине, которые перегорят за срок t. Эта формула дает прекрасное совпадение с фактически наблюдаемым числом вызовов на телефонной станции.

Рассмотрение задач естествознания не с точки зрения качественного, а с позиций их количественного изучения привело к формированию понятия случайного процесса. Первые идеи в этом направлении были высказаны биологами и физиками еще в конце прошлого века. Более определенную форму они приняли в работах физиков А. Фоккера и М. Планка. Однако точное определение случайного процесса и начала теории были построены А. Н. Колмогоровым и А. Я. Хинчиным. Первому из них принадлежит заслуга в создании основ так называемых марковских процессов, второму - стационарных процессов.

Теория вероятностей - наука о случайных явлениях - в настоящее время находится на крутом подъеме. К ней теперь обращаются физики и астрономы, экономисты и лингвисты, биологи и врачи. Без нее не может быть глубокого познания процессов образования помех при радиовещании, правильного расчета организации производства, создания рациональных способов приема больших партий продукции, расчета запасов и средств обороны.

Прогресс теории вероятностей и ее применений требует непрерывного пополнения творчески работающих в ней математиков способной молодежью. Несомненно, среди читателей этой книги будет и та часть молодежи, которая даст новых Лапласов и Чебышевых.

перейти к началу страницы