Зарождение науки о случае

Как и все науки, наука о случае начала развиваться тогда, когда в этом появилась потребность, когда задачи практики уже не могли обходиться выводами, сделанными на глаз, а понадобился точный расчет. Первые шаги в создании теории вероятностей - математической науки о случайных явлениях - были сделаны в середине XVII в., в эпоху зарождения новой математики. Почти одновременно были заложены основы аналитической геометрии и появились ростки, давшие вскоре элементы дифференциального и интегрального исчислений - основы всей современной математики. Этот бурный расцвет математики закономерен. Он был вызван крупными сдвигами в общественных отношениях: развитием торговли, промышленного производства, мореплавания. Первые понятия теории вероятностей формировались под влиянием потребностей страхования и азартных игр. Страхование в ту пору получило широкое распространение из-за непрерывного роста морских сообщений и морской торговли. Азартные игры захватили феодальную верхушку общества. Множество дворян искали в играх способ поправить свои дела. Наряду с большинством бездумных игроков оказались и такие, которые стремились подметить в случайных ситуациях некоторые закономерности. Один из страстных игроков, кавалер де Мере, обратился с рядом возникших у него вопросов к крупнейшему математику и мыслителю того времени Б. Паскалю. Вот один из них. При четырехкратном бросании игральной кости что происходит чаще: выпадет шестерка хотя бы раз или же шестерка не появится ни разу?

Когда-то азартные игры помогли возникновению математической теории.

Посмотрим, как решается эта задача. При бросании одной игральной кости может выпасть одна из 6 граней. В 5 случаях из 6 выпадает грань без шестерки. Если же мы бросим игральную кость один за другим 4 раза, то возможных сочетаний выпавших граней будет значительно больше. Действительно, при двукратном бросании кости число различных сочетаний выпадения граней при первом и втором бросаниях уже будет 36 = 6² (см. таблицу).

Таблица

(1,1)	(1,2)	(1,3)	(1,4)	(1.8)	(1,6)
(2,1)	(2,2)	(2,3)	(2,4)	(2,5)	(2,6)
(3,1)	(3,2)	(3,3)	(3,4)	(3,5)	(3,6)
(4,1)	(4,2)	(4,3)	(4,4)	(4,5)	(4,6)
(5,1)	(6,2)	(5,3)	(6,4)	(5,5)	(5,6)
(6,1)	(6,2)	(6,3)	(6,4)	(6,5)	(6,6)

При бросании кости трижды будет уже 6³ различных сочетаний, а при четырехкратном бросании может представиться 6⁴ = 1296 различных возможностей. При скольких же возможных исходах ни разу не появится шестерка? Из нашей таблички видно, что из 36 возможностей при двукратном бросании кости в 25 случаях (5²) шестерка не появится ни разу. При четырехкратном бросании игральной кости шестерка ни разу не появится в 5⁴ = 625 случаях. Отсюда вытекает, что хотя бы раз при 4 бросаниях шестерка появится в 1296 - 625 = 671 случае. Таким образом, при четырехкратном бросании игральной кости хотя бы раз шестерка появляется несколько чаще, чем ни разу. Это открытие, согласно воспоминаниям современников, не без успеха было использовано кавалером де Мере.

Возникновение основных понятий теории вероятностей и правил действия с ними связано с именами математиков XVII в. Б. Паскаля, П. Ферма, X. Гюйгенса и Я. Бернулли. Те задачи, которые возникали на заре теории вероятностей, сводились примерно к таким ситуациям: при каждом испытании может появиться одно из п одинаково возможных событий. Интересующее нас событие А появляется тогда, и только тогда, когда происходят определенные т из них. Пример: при бросании четырех костей возможны 1296 различных состояний; из них 625 таковы, что при каждом из них ни разу не выпадает шестерка.

Число случаев, при которых наступает интересующее нас событие А, дает нам средство оценки того, как часто оно может наступить при реальных испытаниях. Однако такой способ оценки неудобен, и в науку было введено следующее понятие: вероятностью события А называется отношение числа случаев, при которых событие А наступает, к числу всех возможных случаев. Вероятность события А мы обозначим символом Р { А }. Итак, по определению

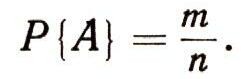
В нашем примере вероятность того, что при 4 бросаниях ни разу не выпадет шестерка, равна:

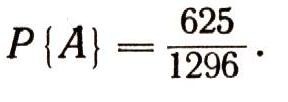
Вероятность же того, что шестерка выпадет хотя бы один раз, равна 671/1296. Рассмотрим теперь еще одну задачу, относящуюся ко времени возникновения теории вероятностей. (Рассказывают, что с этой задачей обратился к X. Гюйгенсу один из ландскнехтов - наемных солдат.) При одновременном бросании трех игральных костей какая сумма выпавших на них очков должна появляться чаще - 11 или 12? Ландскнехт заметил, что и та и другая сумма может осуществиться шестью различными способами, а именно:

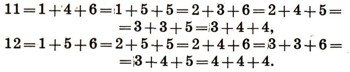
Словами: сумма 11 может появиться только тогда, когда или на одной из костей появляется 1, на другой - 4 и на третьей - 6, или и т. д. Точно так же 12 может появиться только тогда, когда или на одной кости появится 1, на другой - 5, на третьей -6, или и т. д. Казалось бы, 11 и 12 должны появляться одинаково часто, предполагал ландскнехт, однако его долголетний опыт учит другому: 11 появляется несколько чаще, чем 12. В чем же здесь причина?

Мы уже знаем, что всех различных исходов при бросании трех игральных костей будет 216. Теперь задача состоит в том, чтобы подсчитать число всех одинаково возможных исходов, при которых в сумме появляется 11 и 12. Мы увидим при этом, что одинаковое число разложений 11 и 12 на сумму трех слагаемых еще не является достаточным основанием для заключения равенства вероятностей этих событий. Все дело в том, что не все эти суммы одинаково часто встречаются. Так, все суммы, в которых все три слагаемых различны при подсчете числа возможных исходов, должны быть взяты с большим весом, чем остальные. Действительно, разложение 11 на сумму слагаемых 1 + 4 + 6 может произойти шестью различными способами: (1, 4, 6), (1, 6, 4), (4, 1, 6), (4, 6, 1), (6, 1, 4), (6, 4, 1). Мы мысленно нумеруем кости и на первом месте указываем число очков, выпавших на первой кости, на втором - на второй кости и на третьем - на третьей.

Точно так же суммы, в которых два слагаемых одинаковы, например 1 + 5 + 5, могут осуществиться лишь тремя различными способами: (1, 5, 5), (5, 1, 5), (5, 5, 1). И наконец, сумма 4 + 4 + 4 осуществляется одним-единственным способом: (4, 4, 4).

Если теперь учтем только что сказанное, то окажется, что число случаев, при которых в сумме появляется 11, равно: 6 + 6 + 6 + 3 + 3 + 3 = 27, а при которых появляется 12, равно: 6 + 6 + 6 + 3 + 3 + 1 = 25. Таким образом, получаем:

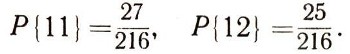
Мы теперь же должны сказать, что расширение области применений теории вероятностей убедительно показало недостаточность того классического определения вероятности, которым мы пользовались, и установило необходимость широкого его обобщения. Такое обобщение сейчас уже произведено, и пока оно удовлетворяет всем запросам как практиков, так и теоретиков. Тем не менее классическое определение вероятности оказалось исключительно полезным для современного естествознания - оно лежит в основе многих важных выводов.

перейти к началу страницы