Исследование операций

Исследование операций - это наука о математическом обосновании решений. Что такое "решение", знает каждый. Пусть имеется ситуация (положение, стечение обстоятельств), в которой перед нами возникает вопрос: Как поступить? Какой образ действий выбрать? Если мы выбираем в данной ситуации определенный образ .действий из ряда возможных, это и называется решением.

Необходимость принимать решения так же стара, как само человечество. Вероятно, еще в каменном веке люди, отправляясь на охоту, принимали решения, например: Чем вооружиться? Какой район леса выбрать? Разделиться ли на две группы или идти всем вместе? И так далее.

Однако до поры до времени решения принимались без всяких научных расчетов, просто на основе опыта и здравого смысла. В ряде случаев такой способ принятия решений устраивает нас и до сих пор. Скажем, человек выходит утром из дому, чтобы ехать на работу. По ходу дела ему приходится принять целый ряд решений: Надевать плащ или нет? В каком месте перейти улицу? Ехать автобусом, троллейбусом или, может быть, трамваем? Все такие решения человек принимает мгновенно (часто бессознательно), опираясь на имеющийся у него опыт и здравый смысл. Здесь никакая наука не нужна и вряд ли понадобится в дальнейшем.

А теперь возьмем другой пример: пусть речь идет об организации работы городского транспорта в большом городе с миллионным населением. Нужно принять ряд решений: Какое количество и каких транспортных средств (автобусов, троллейбусов, трамваев) направить по каким маршрутам? Где расположить остановки? Как часто пускать машины в разное время суток? И т. д.

Здесь решения гораздо сложнее, чем в первом примере, а главное, от них гораздо больше зависит. В первом примере неудачный выбор решения затронет интересы одного человека, во втором - может отразиться на деловой жизни целого города. Такие ответственные решения уже нельзя принимать наобум - для них требуются специальные расчеты. Эти расчеты позволяют избежать риска, заранее оценить сильные и слабые стороны каждого решения и выбрать то из них, которое является наилучшим (или, как говорят, оптимальным). Чем сложнее, чем дороже мероприятие, которое мы собираемся предпринять, тем менее допустимы в нем произвольные, "волевые" решения, опирающиеся только на "опыт и здравый смысл". В особенности когда речь идет о мероприятии, которое вообще проводится впервые! Здесь "опыт" молчит, а "здравый смысл" легко может ввести в заблуждение. Нет уж, лучше "семь раз примерь, один раз отрежь"! Такой предварительной "примеркой" перед выбором решения и служат математические расчеты - исследование операций.

Подобными расчетами люди занимались от случая к случаю с самых давних пор, но в наше время они стали более массовыми и необходимыми, так как сами мероприятия стали более сложными и ответственными. Что касается названия "исследование операций", то оно появилось сравнительно недавно, в годы второй мировой войны, когда в вооруженных силах США и Англии были созданы специальные научно-исследовательские группы, в задачи которых входила подготовка разумных решений по организации боевых операций различных родов войск. В настоящее время это название укрепилось за всеми расчетами по обоснованию решений, к какой бы области практики они ни относились. Математические методы исследования операций применяются сегодня в экономике, промышленности, сельском хозяйстве, в медицине и биологии, в градостроительстве, инженерном деле и транспорте - одним словом, везде, где людям приходится организовывать сложные мероприятия и принимать решения. За последние годы исследование операций развивается очень быстрыми темпами и завоевывает себе все более широкое поле применений. Знакомство с математическими методами исследования операций требуется сейчас от инженеров, научных работников, хозяйственных руководителей. Широкое развитие и применение методов исследования операций опирается в наши дни на вычислительную технику - на быстродействующие электронные цифровые машины (ЭЦВМ), позволяющие в сжатые сроки осуществлять огромный объем расчетов, связанных с переработкой информации о состоянии дела и с оптимизацией решений.

Чтобы дать представление о задачах исследования операций, рассмотрим несколько примеров таких задач.

Рис. 1.

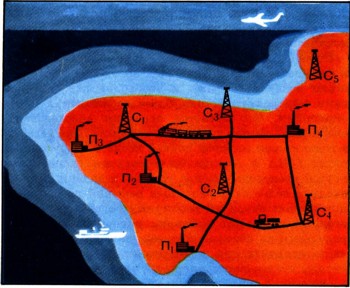
1. Имеется группа промышленных предприятий П₁, П₂, П₃, П₄, расположенных в определенных географических пунктах (рис. 1). Эти предприятия нужно снабжать сырьем. Источники сырья С₁, С₂, С₃, С₄, С₅ также размещены в разных географических пунктах и связаны с предприятиями какими-то путями сообщения (железнодорожными, шоссейными, водными, воздушными) со своими тарифами. Требуется разумным образом разместить заказы на сырье так, чтобы потребности предприятий были удовлетворены в заданные сроки и при этом расходы на перевозку сырья были наименьшими (минимальными).

2. Организуется продажа сезонных товаров (купальных костюмов, шапочек, защитных очков и т. д.). Требуется выбрать количество и вид товаров, число торговых точек, их размещение и т. д., с тем чтобы прибыль за сезон была наибольшей (максимальной).

3. Для обеспечения телевизионной связи запускается серия искусственных спутников Земли. Требуется выбрать количество спутников, их орбиты, тип оборудования и т. д. так, чтобы заданное качество и объем передач были обеспечены при минимальных расходах.

4. Необходимо к определенному сроку произвести обследование большой группы населения для того, чтобы выявить некоторые виды заболеваний. На обследование выделены какие-то средства (врачебный персонал, оборудование, деньги). Требуется разработать план обследования (число медпунктов, их размещение, способ работы, вид и количество анализов и т. п.), с тем чтобы выявить максимальный процент заболевших.

5. Завод изготовляет определенного вида изделия (телевизоры или, скажем, подшипники). Для обеспечения их высокого качества организуется система контроля, причем изделия (все или некоторые) подвергаются каким-то испытаниям (тестам). Требуется рациональным образом организовать этот контроль, т. е. назначить вид тестов, их последовательность, правила браковки и т. д., так, чтобы обеспечить заданный уровень качества изделий при минимальных расходах.

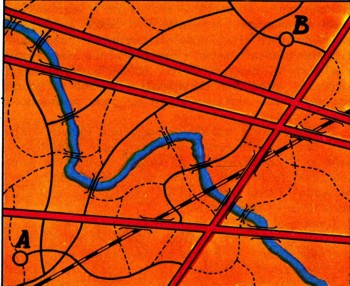
6. Требуется проехать на автомашине из пункта А в пункт В (рис. 2); пункты соединены сетью дорог разного качества: первоклассные благоустроенные шоссе, дороги среднего качества и проселки. Некоторые из них пересекают реки и железнодорожные пути, причем на переездах могут возникать "пробки" (скопления машин). Требуется проложить такой маршрут, по которому машина придет из пункта А в пункт В за кратчайшее время.

Рис. 2.

Как видно, наши примеры взяты из самых разных областей, и все же в них есть что-то общее, а именно: в каждом из них идет речь о каком-то мероприятии, преследующем определенную цель. Заданы какие-то условия, в которых проводится мероприятие (в частности, ресурсы или средства, которыми мы располагаем). В рамках этих условий требуется принять решение так, чтобы наше мероприятие было в каком-то смысле наиболее выгодным (или наименее убыточным). Все эти задачи относятся к области исследования операций, и перечисленные черты являются для них общими и типичными.

Познакомимся с терминологией и основными понятиями исследования операций. Под операцией в широком смысле слова понимается любое мероприятие (или система мероприятий), направленное к определенной цели, заранее спланированное и руководимое из единого центра. Этим мероприятием мы можем в какой-то мере управлять, выбирая зависящие от нас параметры Х₁, Х₂..., которые мы будем называть элементами решения. Если мы выбрали определенным образом все эти параметры, это будет значить, что мы приняли решение.

Решение может быть удачным или неудачным, обеспечивать больший или меньший успех операции. Успешность (или эффективность) операции характеризуется какой-то величиной - мы будем обозначать ее W и называть целевой функцией (иначе - показателем эффективности) операции. Эту величину требуется сделать максимальной (или, наоборот, минимальной). Так, в примере 1 целевой функцией W является стоимость перевозок и ее нужно сделать минимальной. В примере 2 целевой функцией является прибыль и ее, наоборот, надо сделать максимальной. Предлагаем читателю самостоятельно назвать целевую функцию в остальных примерах. Оптимальным решением называется решение, при котором целевая функция обращается в максимум (или в минимум, смотря по смыслу задачи).

Математические методы исследования операций позволяют с помощью расчета заранее выявить оптимальные решения и этим помочь в выборе образа действий тем людям (коллективам), которые несут ответственность за правильную, разумную организацию операции.

Чтобы проанализировать совокупность возможных решений и найти среди них оптимальное, нужно прежде всего построить математическую модель операции, т. е. выразить с помощью каких-то математических формул зависимость между условиями операции "a₁, a₂, ... элементами решения Х₁, Х₂, - и целевой функцией W.

Построение математической модели - самая сложная и ответственная часть исследования. В модели надо по возможности учесть все важные, существенные факторы (причины), от которых зависит успех операции, а менее существенные, второстепенные -отбросить. Чтобы построить правильную, доброкачественную математическую модель, нужно не только хорошо знать математику, но и глубоко разбираться в существе того явления, о котором идет речь. Если математическая модель строится человеком, который имеет о данной области только общее представление, он всегда рискует, с одной стороны, не учесть ряда существенных факторов или учесть их неправильно, а с другой стороны, "утонуть" в несущественных подробностях, излишне усложняющих модель. Наилучшие результаты получаются, когда над моделью работают совместно математики и специалисты в данной конкретной области, к которой относится операция. Для наиболее сложных случаев приходится создавать коллективы специалистов разных профилей - математиков, физиков, инженеров, экономистов, психологов и т. д.

Предположим, что самая трудная и ответственная часть работы по исследованию операций - создание математической модели - выполнена. Это значит, что мы для любых заданных условий а₁, a₂, ... и любого решения (X₁, X₂, ...) можем вычислить целевую функцию W. Запишем зависимость W от условий и элементов решения в виде формулы:

Не нужно думать, что эта зависимость всегда имеет вид простой алгебраической формулы, - нет, часто она гораздо сложнее, например имеет вид уравнения, которое нужно еще решить, или системы графиков, или программы для вычислительной машины, по которой всегда можно вычислить W. Так или иначе, примем, что задача вычисления W решена. Тогда. задачу выбора оптимального решения можно поставить следующим образом:

При заданных условиях а₁, a₂, ... найти такие элементы решения Х₁, Х₂ ..., при которых целевая функция W обращается в максимум (минимум).

Для решения таких задач современная математика разработала много специальных методов, таких, например, как методы линейного программирования, динамического программирования, метод случайного поиска и другие, позволяющие в обозримое время найти оптимальное решение. Надо заметить, что в случаях, когда число элементов решения Х₁, Х₂, ... велико, а целевая функция W зависит от них и заданных условий сложным образом, задача поиска оптимального решения может оказаться в вычислительном отношении очень громоздкой. В настоящее время подавляющее большинство таких задач решается на вычислительных машинах.

Однако вычислительные трудности - это далеко не главные трудности, с которыми приходится встречаться при исследовании операций. Значительно более серьезные затруднения возникают в связи с неопределенностью ситуации.

Представим себе, что обстановка, в которой будет выполняться операция, заранее неизвестна и может оказаться той или другой. Скажем, в задаче о распродаже сезонных товаров (пример 2) успех распродажи существенно зависит от спроса, а спрос -от погоды, которую, как известно, в точности предугадать невозможно, особенно задолго. В задаче о маршруте автомашины (пример 6) тоже нельзя заранее предвидеть, сколько придется простоять машине на том или другом переезде.

Если условия выполнения операции а₁, a₂, ... невсе известны заранее, а среди них есть неопределенные, задача исследования операций превращается в задачу о выборе решения в условиях неопределенности. Трудная задача, но, к сожалению, очень типичная! И встречается она на практике куда чаще, чем случай, когда все условия известны заранее. Как же быть? Отказаться от математического исследования? Ни в коем случае!

Разумеется, неопределенность есть неопределенность, с этим ничего не поделаешь, и любое решение, принятое в условиях неопределенности, хуже того, которое мы приняли бы, если полностью знали обетановку. Приняв решение в условиях неопределенности, мы не гарантированы, что обстановка не обернется против нас, и тогда мы выиграем меньше, чем рассчитывали. И все-таки математические методы помогут нам принять решение более разумное, чем если бы мы действовали просто наобум. Существует ряд приемов, позволяющих принять и в условиях неопределенности решение лучшее, чем остальные.

Прежде всего надо сказать о вероятностных методах анализа случайных ситуаций. Как известно, теория вероятностей занимается закономерностями в случайных явлениях и предсказаниями (прогнозами) в области массовых случайных явлений. Методами теории вероятностей можно найти разумный способ поведения в условиях, которые'могут меняться случайным и непредвиденным образом. Мы можем, например, выбрать такое решение, которое обеспечит нам максимальный средний выигрыш при неоднократном выполнении операции (а многие операции как раз и выполняются неоднократно!). Или, если мы очень боимся риска, неожиданных крупных потерь, можно выбрать такое решение, которое сводит к минимуму вероятность крупной потери. Многого можно достигнуть при математическом исследовании операции даже в условиях неопределенности - нужно только хорошо знать, к чему мы стремимся и чего опасаемся.

Бывают особые обстоятельства, когда неизвестные условия операции зависят не от "слепого случая", а от сознательно противодействующего нам противника (например, в ходе военных действий). В таких задачах найти оптимальное решение помогает специальная наука - теория игр (так называется математическая теория конфликтных ситуаций). Близкими к теории игр задачами занимается теория статистических решений - там рассматривается неопределенность, не обязательно связанная с враждебной деятельностью противника (так называемые "игры с Природой").

Особые сложности в задачах исследования операций возникают, когда успешность операции описывается не одной-единственной целевой функцией (показателем эффективности) W, а сразу несколькими: W₁, W₂ ..., W_k из которых одни желательно сделать побольше (максимизировать), а другие поменьше (минимизировать). Например, организуется работа промышленного предприятия, и нам хотелось бы: а) максимизировать прибыль, б) минимизировать количество занятых на производстве людей, в) максимизировать количество сэкономленного сырья и т. д. Одним словом, хочется, чтобы "и волки были сыты и овцы целы"...

Легко видеть, что поставленные требования противоречивы: максимально удовлетворяя одному из них, мы неизбежно ставим под удар другие. Возникает вопрос о выборе так называемого компромиссного решения, которое, не будучи, может быть, в точности "оптимальным" ни по одному показателю, является приемлемым по всей совокупности показателей. Здесь тоже могут быть применены некоторые математические методы, позволяющие, например, заранее выявить и отбросить те варианты решения, которые уступают другим по всем показателям, со всех точек зрения. После того как эти заведомо негодные варианты решения будут отброшены, уже легче из оставшихся выбрать удачное компромиссное решение, приемлемое по всем показателям.

С некоторыми задачами исследования операций вы можете познакомиться по книжке А. Кофмана и Р. Фора "Займемся исследованием операций".

перейти к началу страницы