Математизация экономической постановки задачи

Предположим, что цех должен выпускать х₁штук продукции вида А и х₂ штук продукции вида В. При этом станков I группы будет использовано 1 * x₁+ 1 * X₂Но в цехе имеется всего 18 станков I группы, следовательно, имеем первое ограничение:

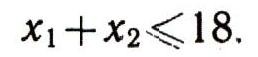
Три остальных ограничения получаются аналогично:

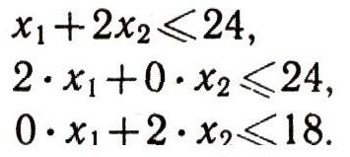
Таким образом, нами получена система четырех линейных неравенств. Нас будут интересовать только неотрицательные (допустимые) решения данной системы (нельзя же практически использовать, например, решение, где х₁ = - 6, эквивалентное тому, что цех должен сделать - 6 штук продукции?!).

х₁штук продукции вида А дадут цеху прибыль 40 * X₁руб., a X₂штук продукции вида В дадут 60-х₂ руб. Общую прибыль будет описывать линейная функция F = 40x₁+60x₂. Нам необходимо среди неотрицательных решений системы линейных неравенств отыскать такое, которое максимизировало бы линейную функцию F.

Математическая формулировка этой задачи выглядит так: Найти максимум линейной функции F = 40x₁+ 60x₂при условии

I решение. В этой задаче только два неизвестных x₁ и x₂. Это позволяет получить решение геометрически. Неравенства (д) и (е) ограничивают поиск решения первым квадрантом (рис. 1).

Рис. 1

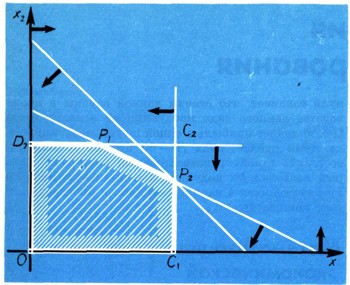
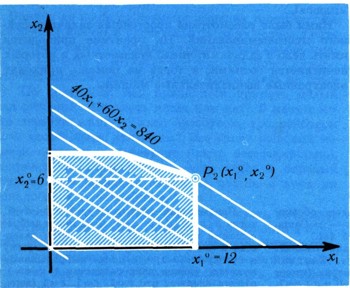
Неравенствам (в) и (г) удовлетворяют лишь точки, находящиеся внутри или на сторонах прямоугольника D₂С₂С₁O. Линейные неравенства (а) и (б) еще сильнее ограничивают область поисков допустимых решений. После наложения всех шести ограничений мы получили многоугольник OD₂P₁P₂C₁, являющийся множеством допустимых решений задачи. Теперь среди множества этих решений надо выбрать такое, при котором линейная функция F достигала бы максимума, т. е. необходимо найти такую точку, принадлежащую этому многоугольнику, чтобы координаты ее (x₁°, x₂°) обращали F в максимум. Приравняем выражение для F, т. е. F = 40x₁ + 60x₂, какой-либо постоянной а: 40x₁ + 60x₂= а.

Рис. 2

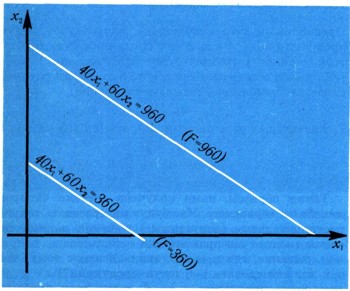
Известно, что это уравнение определяет прямую, в каждой точке которой функция F принимает одно и то же значение а. Пусть а = 360, тогда уравнение 40x₁ + 60x₂= 360 определяет прямую (F = 360) на рис. 2. Если же положить а = 960, то уравнение 40x₁ + 60x₂ = 960 определит другую прямую (F = 960). Если представить, что а, возрастая, принимает значения от 0 до бесконечности, то прямая, соответствующая уравнению 40x₁ + 60x₂ = а, смещаясь параллельно самой себе, образует семейство параллельных прямых. Такое семейство показано на рис. 3, где каждой прямой поставлено в соответствие определенное значение функции F. Направление возрастания значения а показано стрелкой. По взаимному расположению многоугольника допустимых значений и этого семейства прямых можно определить, какая точка многоугольника соответствует наибольшему значению F. Из рис. 4 видно, что такой точкой является точка Р₂. Чтобы определить координаты этой точки, достаточно решить систему уравнений тех прямых, пересечением которых она является: x₁ + x₂=18 x₁ + 2x₂ = 24, x₁ = 12.

Рис. 3

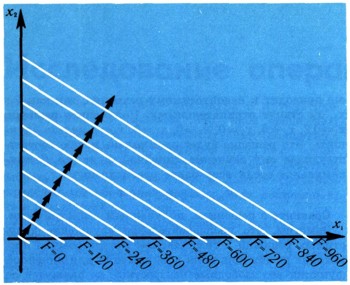
Откуда x₁° = 12, x₂° = 6. При этом допустимом решении F=40x₁ + 60x₂ = 840 (руб.). Это решение оптимальное, ибо ни при каком другом допустимом решении значение линейной функции F не будет большим.

Предлагаем читателю самому убедиться в этом, вычислив для сравнения, например, значение F в точке P₁. Заметим, что в теории линейного программирования доказывается теорема, по которой оптимального значения линейная функция может достигать только на границе многоугольника допустимых решений.

II решение. Теперь решим эту же задачу с помощью симплексного метода. Читателю следует обратить внимание на основную идею этого метода - последовательное улучшение допустимых решений.

Рис. 4

Сначала приведем нашу задачу к виду, удобному для применения симплексного метода. Для этого систему неравенств (1) необходимо преобразовать в систему линейных уравнений. Чтобы неравенство x₁+x₂=<18 превратить в равенство, достаточно в левую его часть ввести дополнительное неотрицательное неизвестное, например, x₃:

x₁+x₂+x₃='18.

Вводя дополнительные неизвестные х₄, x₅ х₆ в остальные неравенства, имеем:

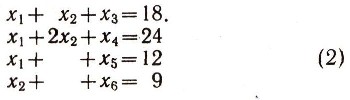
Эта система четырех уравнений имеет шесть неизвестных. Значит, имеется два неизвестных, называемых свободными, через которые можно выразить остальные четыре, называемые базисными. Заметим, что свободные неизвестные неотрицательны. В качестве свободных неизвестных произвольно выбираем х₁и х₂-

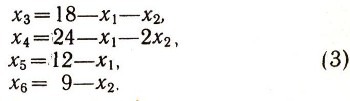
Линейная функция уже выражена через свободные неизвестные: F = 40x₁ + 60x₂. Если придавать свободным неизвестным какие-либо значения, то будем получать все новые и новые решения. В симплексном методе ограничиваются только базисными решениями, т. е. решениями, которые получаются, когда свободные неизвестные равны нулю.

Система (3) имеет такое базисное решение (x₁=0, х₂ = 0, x₃ = 18, x₄ = 24, х₅ = 12, Х₆ = 9), при котором значение линейной функции F=0. При этом допустимом решении цех ничего не должен делать и, естественно, прибыль равна нулю. В выражении для F свободные неизвестные входят со знаком "плюс". Следовательно, их увеличение должно привести и к увеличению F. Будем увеличивать х₁при x₂ = 0. Нас интересуют только допустимые (неотрицательные) решения, поэтому х₁нельзя увеличивать неограниченно, ибо при этом базисные неизвестные x₃, х₄, х₅ могут стать отрицательными (см. систему (3). Из третьего уравнения системы (3) видно, что х₁можно увеличить лишь до 12. Положим теперь x₁=12, тогда х₅ = 0. Это приводит к новому допустимому решению: x₁ = 12, x₂ = 0, x₃=6, x₄=12, x₅ = 0, х₆ = 9, при котором значение линейной функции стало больше: F = 40x₁+ 60x₂ = 480 (руб.).

В этом решении (как и в первом) два неизвестных равны нулю (х₂ и х₅). Будем считать их свободными и выразим через них новое базисное неизвестное х₁. Из третьего уравнения системы (3) имеем: x₁ = 12-х₅.

Подставляя это выражение для х₁в остальные уравнения системы (3) и в выражение линейной функции, получим:

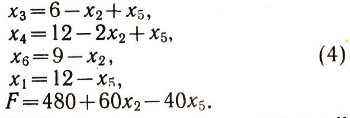
Из системы (4) видно, что увеличение х₂ при x₅ = О будет вести к дальнейшему увеличению значения F. Но первые три уравнения системы (4) ограничивают увеличение х₂. При x₂ = 6 значение линейной функции станет F = 840. Неизвестные х₃и х₄при этом окажутся равными нулю, т. е. станут свободными. Нами получено новое допустимое решение:

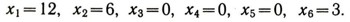
Выразим новое базисное неизвестное x₂ через свободные. Из первого уравнения имеем:

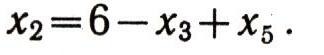
Выражая F через свободные неизвестные, имеем:

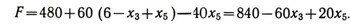
Из этого выражения как будто бы следует, что за счет увеличения х₅ можно добиться еще большего увеличения F. Выразим базисные неизвестные системы (4) через свободные неизвестные х₃ и х₅:

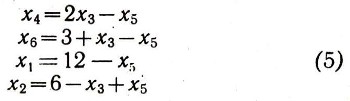
Анализ уравнений системы (5) показывает, что любое увеличение неизвестного x₅ при x₃= 0 сразу же приводит к недопустимому решению, так как х\, x₄, x₆ станут отрицательными. Полученное решение x₁=12, x₂ = 6, x₃ = 0, x₄ = 0, x₅ = 0, x₆ = 3 нельзя улучшить. Это решение будет оптимальным, ибо соответствующее ему значение линейной функции F максимальное среди всех ранее рассмотренных. F_mаx=840 (руб.). Сравните с решением, полученным геометрически.

Заметим, что последовательное улучшение допустимых решений в симплексном методе обычно происходит до тех пор, пока в выражении для линейной функции все свободные неизвестные не окажутся со знаком "минус" (в случае минимизации - со знаком "плюс").

Нами была рассмотрена простейшая задача линейного программирования. На практике приходится иметь дело с задачами, число неизвестных в которых исчисляется сотнями, и тогда на помощь приходят электронные вычислительные машины.

Решение к стр. 381. Введем обозначения : а - Саша, b - Костя, с - не Саша, d - 18 лет, е - 21 год и f - 25 лет.

Мама сказала: "а*е", папа сказал: "b*d", а дочь сказала: "с*f". Так как часть каждой информации неверна (имеет значение 0), то а*e=b*d=c*f=0 и а+е=1, b+d=l, c+f=l.

Сын Николая Ивановича не может иметь сразу два имени и два возраста; следовательно: a*b=a*c=d*e=d* е=е*f=0.

Перемножим суммы а+е=1 я b+d=l, тогда а * b + а * d+b * е+е * d=l, после выбрасывания нулевых членов останется равенство a*d+b*e=l. Перемножим эту сумму и сумму с+f=1, что после выбрасывания нулевых членов даст равенство b*с*е=1, откуда следует, что b = 1, с=1, е=1(верхняя информация). Значит, сына Николая Ивановича зовут не Саша (с=1), а Костя (b = 1) и возраст его 21 год (е=1).

Интересное свойство числа 121

Запись 121 имеет смысл числа не только в десятичной системе, но и в любой другой, основание которой В>2. Это число интересно тем, что является полным квадратом как при основании 10 (121 = 11²), так и при любом другом основании В>2. Докажите!

Пять зашифрованных действий

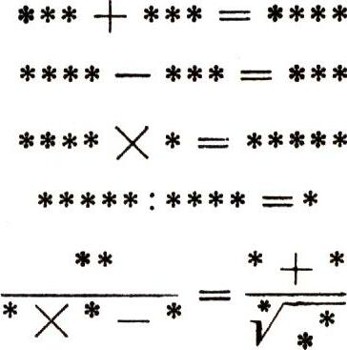
Расшифруйте эти пять равенств, заменяя звездочки цифрами так, чтобы в каждом равенстве появились все 10 цифр от О до 9. Числа, образующие первые четыре действия, не должны совпадать.

перейти к началу страницы