Симметрия в природе

Симметрией обладают не только геометрические фигуры или вещи, сделанные рукой человека, но и многие творения природы (бабочки, стрекозы, листья, морские звезды, снежинки и т. д.). Особенно разнообразны свойства симметрии кристаллов. На рис. 8 показаны некоторые виды кристаллов. Одни из них более симметричны, другие - менее. Долгое время ученые-кристаллографы не могли описать всех видов симметрии кристаллов. Решил эту задачу в 1890 г. русский ученый Е. С. Федоров. Он доказал, что есть ровно 230 групп, переводящих в себя кристаллические решетки. Это открытие значительно облегчило кристаллографам изучение видов кристаллов, которые могут существовать в природе.

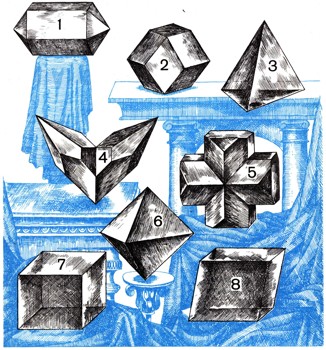
Следует, однако, заметить, что многообразие кристаллов в природе настолько велико, что даже использование группового подхода не дало еще способа описать все возможные формы кристаллов. Очень широко используется теория групп симметрии в квантовой физике. Уравнения, которыми описывается поведение электронов в атоме (так называемое волновое уравнение Шредингера), уже при небольшом числе электронов настолько сложны, что непосредственное решение их практически невозможно. Однако, используя свойства симметрии атома (неизменность электромагнитного поля ядра при поворотах и симметриях, возможность перестановки некоторых электронов между собой, т. е. симметричное расположение этих электронов в атоме, и т. д.), удается исследовать их решения, не решая уравнений.

Примером симметрии в природе является одуванчик.

Вообще, использование теории групп является мощным математическим методом исследования и учета симметрии явлений природы.

перейти к началу страницы