Что такое равные фигуры

В статье "Геометрические преобразования" рассказано, что две геометрические фигуры называются равными, если существует движение, при помощи которого можно совместить одну фигуру с другой. Геометрические свойства равных фигур совершенно одинаковы. Поэтому можно сказать, что геометрия изучает только те свойства фигур, которые не меняются при движениях.

Однако это определение не всегда удовлетворительно. Например, при изучении векторов (а теория векторов - это часть геометрии) два вектора считают равными, если не только их длины одинаковы, но и векторы параллельны и одинаково направлены.

Поэтому, например, векторы

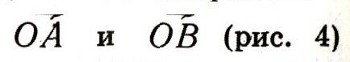
не считаются равными, хотя один из них получается из другого поворотом вокруг точки О. А векторы ОА и CD на том же рисунке равны друг другу. Чтобы получить вектор CD из вектора ОА, надо сделать параллельный перенос плоскости на вектор ОС.

Таким образом, два вектора называются равными, если один получается из другого с помощью параллельного переноса. Можно сказать, что векторная алгебра изучает свойства, остающиеся неизменными при параллельных переносах.

Рис. 2

В других случаях приходится изучать свойства фигур, остающиеся неизменными лишь при поворотах вокруг некоторой точки. Если, например, инженеру надо рассчитать турбину, то для него все лопатки турбины равноправны - одна - получается из другой поворотом вокруг оси турбины. А сместить лопатку вдоль радиуса нельзя - при этом изменится центробежная сила и весь расчет окажется неверным.

Точно так же две фигуры на сфере надо считать равными, если одна получается из другой поворотом вокруг центра сферы.

Рис. 3

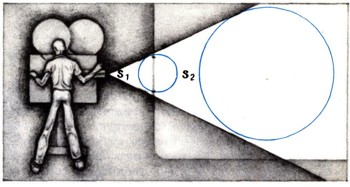
Можно привести и такие случаи, когда целесообразно считать равными геометрические фигуры, не являющиеся таковыми с обычной точки зрения. Например, при изучении угловых свойств окружности можно полностью отвлечься от ее размеров. Тогда все окружности будут для нас одинаковыми. Но окружность S₁ на рис. 5 нельзя перевести в окружность S₂ движением. Для этого надо применить более общее преобразование подобия. Существуют и такие случаи, когда целесообразно считать равными фигуры, переводимые друг в друга линейными и другими преобразованиями (см. об этом подробнее в статье "Геометрические преобразования").

Рис. 4.

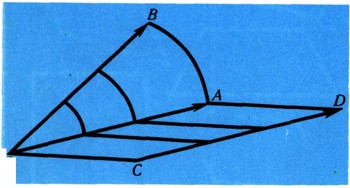
Поэтому можно дать такое определение равенства геометрических фигур. Пусть имеется некоторое множество геометрических преобразований G. Фигура F₁ называется равной фигуре F₂ относительно этого множества преобразований, если есть преобразование а из G, переводящее F₁ в F₂. Например, если множество G состоит из параллельных переносов, то фигуры F₁ и F₂ на рис. 6 равны, а фигуры F₁ и F₃ не равны. Если же множество G состоит из поворотов вокруг точки О, то равными окажутся фигуры F₁ и F₃, а неравными - F₁ и F₂. Наконец, если взять множество всех движений плоскости, то относительно него все три фигуры равны.

Рис. 5

Рис. 6

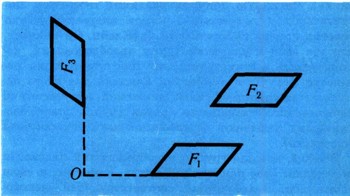
Ясно: чем больше преобразований содержит множество G, тем большее число фигур окажется равным относительно этого множества преобразований.

перейти к началу страницы