Циркуль и линейка

На развитие теории уравнений сильное влияние оказали задачи о построениях циркулем и линейкой, в особенности задачи о построении правильных многоугольников. Из школьного курса известно, как строить циркулем и линейкой правильный треугольник, квадрат и шестиугольник. В более подробных курсах рассказано о построении правильного пятиугольника. А вот о построении правильного семиугольника или девятиугольника ничего не говорится. И это не случайно: ни правильный семиугольник, ни правильный девятиугольник нельзя построить циркулем и линейкой.

Как же это узнали? Ведь доказать разрешимость задачи сравнительно легко - достаточно указать путь ее решения. Доказать же, что задачу нельзя решить, очень трудно. Путей решения задачи бесконечно много (мало ли какие построения можно придумать!), и доказать, что ни один из них не приведет к цели, на первый взгляд невозможно.

Однако математики справились с этой задачей. Для этого они сначала исследовали вопрос, какие отрезки можно построить циркулем и линейкой исходя из одного заданного отрезка (в случае построения правильного многоугольника заданным является радиус описанной окружности или сторона искомого правильного многоугольника).

Чтобы ответить на этот вопрос, пришлось ввести понятие квадратичной иррациональности. Так назвали числа, которые получаются из единицы с помощью четырех арифметических действий и операции извлечения квадратного корня. Вот для примера некоторые числа, являющиеся квадратичными иррациональностями:

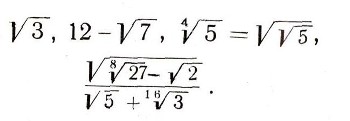
Все квадратичные иррациональности, вместе взятые, образуют числовое поле, причем в этом поле всегда выполнима операция извлечения квадратного корня из положительного числа. Было доказано, что если задан отрезок а, длина которого принимается за единицу, то циркулем и линейкой можно построить любые отрезки, длины которых являются квадратичными иррациональностями, и только эти отрезки.

Например, для построения правильного пятиугольника с данной стороной достаточно построить его диагональ (тогда все вершины можно будет найти с помощью засечек окружности). Расчеты показывают, что если сторона пятиугольника равна 1, то его диагональ имеет длину

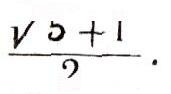
Так как это число является квадратичной иррациональностью, то построение правильного пятиугольника с помощью циркуля и линейки возможно. А вот правильный девятиугольник построить нельзя. Эта задача сводится к построению угла в 40°. Нетрудно проверить далее, что число cos40° является корнем уравнения

Было доказано, что если один из корней кубического уравнения с целыми коэффициентами является квадратичной иррациональностью, то у него есть и рациональный корень. А легко доказать, что у уравнения (3) рациональных корней нет, значит, нет и корней, являющихся квадратичными иррацио-нальностями. Поэтому и нельзя построить правильный девятиугольник циркулем и линейкой.

Окончательное решение вопроса о построении правильных многоугольников циркулем и линейкой дал в 1796 г. Гаусс. Он доказал, что если р - простое число, то правильный р-угольник с данной стороной может быть построен циркулем и линейкой в том, и только том, случае, когда число р можно записать в виде р - 2²ⁿ + 1, где п - целое число. Например, при п = 0 имеем р - 3, а при п = 1 имеем р=5. Поэтому правильный треугольник и правильный пятиугольник можно построить циркулем и линейкой. При n = 2 получаем р = 17. Значит, и правильный семнадцатиугольник строится циркулем и линейкой. Можно построить циркулем и линейкой даже правильные многоугольники с 257 и 65 536 сторонами. А вот при п = 5 число 2²ⁿ + 1 оказывается составным. Поэтому правильный (2²⁵ +1) - угольник нельзя построить циркулем и линейкой.

В древности математики потратили много сил на решение следующей задачи об удвоении куба: дан куб со стороной а; построить такой куб, объем которого вдвое больше объема данного куба. Примем длину отрезка а за единицу, а длину ребра искомого куба обозначим через х. По условию задачи должно быть х³ = 2. Это уравнение не имеет рациональных корней. Поэтому по упомянутой выше теореме у него нет и корней, являющихся квадратичными иррацио-нальностями. Значит, решить задачу удвоения куба циркулем и линейкой невозможно.

Гораздо труднее было доказать, что невозможно построить циркулем и линейкой квадрат, равновеликий кругу радиуса 1 (задача о квадратуре круга). Это доказательство было проведено неалгебраическими методами. Было доказано, что сторона такого квадрата не только не является квадратичной иррациональностью, но даже не может быть корнем никакого алгебраического уравнения с целыми коэффициентами (такие числа называют неалгебраическими или трансцендентными).

перейти к началу страницы