Основная теорема алгебры многочленов

Мы видели, что чем богаче элементами поле Р, тем больше возможностей разложить над ним заданный многочлен f(x) на множители. Например, многочлен x⁴ - 2 совсем не разлагается над полем рациональных чисел, но разлагается на три множителя над полем действительных чисел:

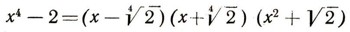
и на четыре - над полем комплексных чисел:

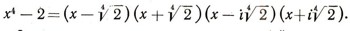
Однако расширение поля влечет за собой и расширение множества многочленов, которые надо разлагать. Ведь если допустить в качестве коэффициентов не только рациональные, но и действительные числа, то придется разлагать не только такие многочлены, как x⁴ - 2, но и такие, как х⁴ - корень из 2, и даже такие, как х⁴ - Пи. А если допустить комплексные числа, то придется рассматривать и многочлены вида x⁴ + i.

К счастью, оказалось, что выигрыш от расширения поля больше, чем проигрыш, - над полем комплексных чисел любой многочлен (не только с рациональными, но и с любыми комплексными коэффициентами) разлагается до конца, т. е. на множители первой степени. А это означает, что всякое уравнение л-й степени с комплексными коэффициентами имеет ровно п корней. Эту теорему называют основной теоремой алгебры многочленов. Ее доказал К. Гаусс в 1799 г.

Сложнее обстоит дело с разложением многочлена над полем действительных чисел. Как мы видели, над этим полем многочлен х² + 6х + 10 не разлагается на множители первой степени. Однако любой многочлен с действительными коэффициентами, степень которого больше двух, всегда разлагается на множители с коэффициентами того же вида. Поэтому всякий многочлен с действительными коэффициентами разлагается над полем действительных чисел на множители первой и второй степеней.

перейти к началу страницы