Разложение многочленов на множители и решение уравнений

Зачем же надо разлагать многочлены на множители? Одна причина ясна - для выполнения действий с алгебраическими дробями. Но есть и другая причина - разложение на множители облегчает решение уравнений. Пусть нам дано уравнение:

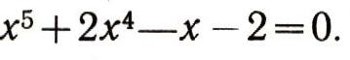
Решать уравнения пятой степени мы не умеем. Но если сгруппировать члены в левой части, то получим:

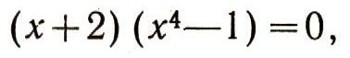
или

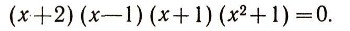
А теперь видно, что левая часть обращается в нуль при х₁ = 2, x₂ = 1, x₃= -1. Значит, эти числа являются корнями нашего уравнения. Других действительных корней у него нет, так как произведение может равняться нулю, лишь если какой-нибудь множитель равен нулю, а множитель х²+1 при действительных х в нуль не обращается.

Особенно легко решать уравнения, левая часть которых разложена на множители первой степени:

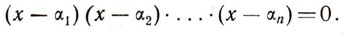
В этом случае ясно, что корнями будут числа а₁, а₂, ..., а_n а других корней не будет (так как если х отлично от всех чисел а₁, a₂, ... а.., то ни один из множителей первой степени в нуль не обращается). Верно и обратное: если мы знаем п корней оц, а₂. ..., а многочлена

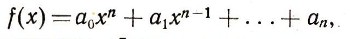
то он следующим образом разлагается на множители:

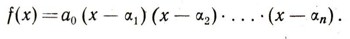
Из сказанного ясно, что никакое уравнение л-й степени не может иметь больше, чем п корней. А имеет ли любое уравнение хотя бы один корень? Впрочем, эта задача опять нечетко поставлена: неясно, что значит "любое уравнение", Какими должны быть его коэффициенты. Неясно и то, какие корни мы будем рассматривать.

перейти к началу страницы