Разложение чисел на множители

С разложением чисел на множители вы знакомы. Вам приходится это делать при отыскании общего знаменателя, при сокращении дробей и т. д.

Одно из основных утверждений арифметики гласит: каждое натуральное число единственным образом разлагается на простые множители. Например: 72=2*2*2*3*3; 1001=7*11*13 (разумеется, разложения, отличающиеся лишь порядком множителей, мы считаем одинаковыми). Напомним, что простым числом называется натуральное число, имеющее только два различных делителя (само число и 1). Число 1 не считается простым.

Будем теперь рассматривать не только натуральные числа, но и нуль и отрицательные целые числа. Иными словами, возьмем множество всех целых чисел. На первый взгляд здесь труднее определить понятие простого числа. Ведь, например, 7 = ( - 1)*( - 7). Значит ли это, что число 7 перестает быть простым, если его рассматривать в множестве всех целых чисел? Оказывается, нет, надо только уточнить, что называется простым числом.

Заметим, что число - 1 обладает следующим свойством: если разделить 1 на -1, то в частном получится целое число. Другим целым числом с таким же свойством является сама единица. Мы будем называть эти числа (1 и - 1) делителями единицы.

Назовем целое число р простым, если оно не является делителем единицы, но в любом его разложении в произведение двух целых множителей один из сомножителей обязательно является делителем единицы. При таком определении число 7 остается простым и после перехода к множеству всех целых чисел. Простым будет и число - 7.

Сохраняет свою силу и основной закон арифметики, однако тоже с небольшим изменением формулировки: каждое целое число, отличное от нуля, разлагается в произведение простых целых чисел; это разложение однозначно определено с точностью до перестановок сомножителей и возможного умножения некоторых сомножителей на - 1 (т. е. на делитель единицы). Например: 21=3*7 = 7*3=(-3)*(-7) = (-7)*( -3). Такие разложения принято считать одинаковыми.

Удивительное разложение

При решении некоторых сложных вопросов теории чисел пришлось разлагать целые числа не только на целые множители, но и на множители вида

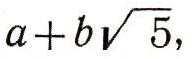
где а и о - целые числа. Числа такого вида сами образуют кольцо. Для них, как и для целых чисел, можно определить понятия простого числа, делителя единицы и т. д. Например, число

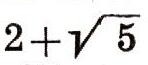
- делитель единицы, так как

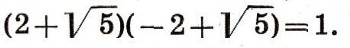
Велико же было удивление математиков, когда оказалось, что в кольце чисел

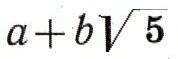
нарушается основной закон арифметики о единственности разложения на простые множители. Например:

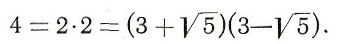
А вот в кольце чисел вида

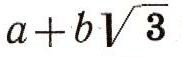
(а и b - целые) имеются делители единицы кроме 1 и -1, например:

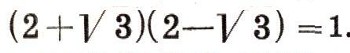
Но разложение на множители в этом кольце однозначно (как всегда, с точностью до перестановки множителей и умножения этих множителей на делители единицы).

В теории чисел полностью изучен вопрос, в каких кольцах чисел вида

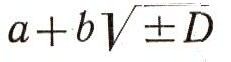
имеет место однозначность разложения на простые множители, а в каких нет. Мы не будем на этом останавливаться.

перейти к началу страницы