Сила букв

Уже пятиклассники хорошо понимают, насколько алгебра сильнее арифметики: вместо того чтобы решать несколько задач, отличающихся только числовыми данными, можно решить одну задачу с буквенными данными, а потом подставлять в полученный ответ различные числовые данные.

При этом полученный алгебраический ответ часто можно упростить, пользуясь правилами алгебраических преобразований, и тогда подставлять числовые данные и производить арифметические действия будет гораздо проще.

На этом факте основаны многочисленные "фокусы" с отгадыванием задуманных чисел. Например, предложим выполнить следующие действия: 1) задумайте число; 2) прибавьте к задуманному числу 5; 3) полученный результат умножьте на 3; 4) отнимите от получившегося теперь результата задуманное число; 5) отнимите 11; 6) разделите полученный ответ на 2. Если сообщить "фокуснику" полученный результат, то он сразу назовет задуманное число. При этом ему не придется выполнять в обратном порядке всей сложной последовательности действий. В самом деле, если обозначить задуманное число через х, то действия, которые предложено выполнить, запишутся следующим образом:

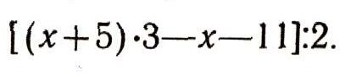
Упрощая это выражение, легко найдем, что оно равно х + 2. Поэтому "фокуснику" достаточно отнять от сообщенного ему результата 2, чтобы получить задуманное число.

Однако шестиклассник (да и оканчивающий школу) не оценивает полностью всю силу буквенных формул. Он считает, что буквы в них - это обязательно какие-то числа (заранее известные или искомые). На самом же деле, производя действия с буквами, он использует лишь аксиомы алгебры и их следствия. Поэтому все его вычисления годятся не только для чисел, но и для любых вещей, для которых выполняются эти аксиомы. Например, буквы могут означать не отдельные числа, а многочлены, алгебраические дроби и другие алгебраические выражения.

Ведь хорошо известно, что для сложения и умножения многочленов выполняются те же аксиомы (1), что и для сложения и умножения чисел. Например, если а и b - некоторые многочлены, то a + b = b + a, ab = ba и т. д. Отсюда следует, что в любое алгебраическое тождество вместо букв можно подставлять не только числа, но и любые многочлены. Например, из того, что

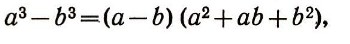
следует тождество

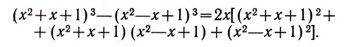
Если кроме чисел и многочленов нам встретятся другие вещи, которые можно складывать и умножать, причем выполняются аксиомы (1), то для них будут верны все формулы и выводы алгебры. Например, старшеклассники встречаются с комплексными числами. Верны ли для таких чисел формулы алгебры, или надо снова выяснять, чему равен куб суммы комплексных чисел? Из сказанного следует, что проверять заново для комплексных чисел все формулы алгебры не нужно. Достаточно проверить аксиомы (1), а из них уже будут следовать все остальные формулы.

перейти к началу страницы