Фундамент алгебры

Из всех сделанных высказываний школьнику Васе Игнатьеву, который был корреспондентом школьной стенгазеты и присутствовал на конференции, самым правильным показалось мнение алгебраиста XVII в., что алгебра - искусство буквенных вычислений.

Вася учился тогда в VI классе и на уроках алгебры много занимался буквенными вычислениями. Тут были и формулы сокращенного умножения, и коэффициенты, и показатели степени, и многое другое -от букв в глазах рябило. Он часто думал: "Хорошо было бы иметь решения ко всем примерам нашего задачника!" Но вскоре понял, что это не поможет, -учитель для контрольных работ брал примеры из какого-то другого задачника. А запомнить решения всех задач из всех задачников на свете - это, пожалуй, никому не под силу, разве что фокусникам из цирка, выступающим с сеансами феноменальной памяти.

Делать нечего, приходилось заучивать правила: что происходит с коэффициентами и показателями при умножении одночленов, как возводить сумму и разность в квадрат и многое другое.

Вася был мальчик любознательный и захотел узнать, откуда же эти правила берутся. Внимательно читая учебник, он понял, что все правила, по которым выполняются действия с многочленами, вытекают из небольшого числа основных правил. Эти первоначальные правила таковы :

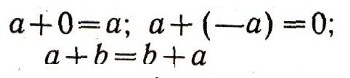
(коммутативность сложения);

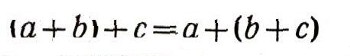
(ассоциативность сложения);

(коммутативность умножения);

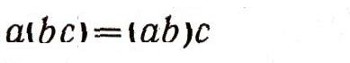
(ассоциативность умножения);

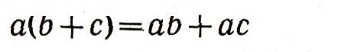
(дистрибутивность). Из этих правил можно вывести все остальные, например формулу

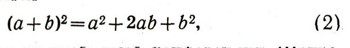
обсуждавшуюся на необычной конференции. (Попробуйте это сделать!)

Таким образом, искусство буквенных вычислений сводится к применению основных правил. При этом некоторые следствия из этих правил (например, формула квадрата суммы) применяются настолько часто, что их надо так же хорошо запомнить и применять, как и первоначальные правила.

Не правда ли, это очень напоминает положение дел в геометрии - там тоже есть несколько аксиом (т. е. первоначальных положений), из которых выводятся различные следствия, называемые теоремами. А при решении задач приходится применять и аксиомы и теоремы. Поэтому мы будем, как и в геометрии, формулы (1) называть аксиомами, а формулы вида (2) - теоремами.

Как и аксиомы геометрии, аксиомы алгебры не доказываются. Они являются обобщением многотысячелетнего опыта практической деятельности человечества. Прежде чем сформулировать положение a + b = b + a, надо было много тысяч раз подметить такие арифметические соотношения, как: 2 + 5 = 5 + 2, 4 + 6 = 6 + 4 и т. д.

Все остальные аксиомы (1) имеют такое же происхождение: они являются буквенной записью многократно проверявшихся законов арифметики.

перейти к началу страницы