Необычная конференция

Алгебраист XVI в. записал формулу квадрата суммы так, как показано на рис. 1.

Вообразим, что нам удалось собрать математиков разных веков и стран и поставить перед ними вопрос: "Что вы можете сказать о формуле квадрата суммы?" Стенограмма этой необычной конференции могла бы выглядеть примерно так.

Вавилонский математик, живший 4000 лет назад, сказал, что никаких формул он не знает, так как выполняет действия не над буквами, а над числами. Но ему известно, что если взять два числа, например 20 и 3, то для вычисления квадрата их суммы надо возвести в квадрат число 20, потом число 3, сложить эти квадраты и к сумме прибавить удвоенное произведение чисел.

Древний грек, живший 2300 лет назад, доказал это правило. Он нарисовал квадрат, разбил его на два квадрата и два равных прямоугольника (см. рис. слева) и сказал, что площадь квадрата АС (т. е. квадрата, у которого точки А и С являются концами диагонали) равна сумме площадей квадратов АВ и ВС и удвоенной площади прямоугольника BD. Поэтому если сторона квадрата АВ равна 20, а квадрата ВС равна 3, то площадь квадрата АС действительно можно подсчитать так, как предложил его вавилонский коллега.

В переводе это читалось бы примерно так:

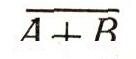
в квадрате равно А в квадрате +В в квадрате +А на В2. (Вместо скобок он писал черту, степени обозначал словами, а коэффициенты писал в конце.) - Не слишком удобные обозначения, - сказал иронически математик XVII в. - Однако и с этими обозначениями мы умеем делать значительно больше, чем древние греки, -с обидой возразил выступавший. - Они умели решать лишь квадратные уравнения, а мы справляемся и с уравнениями третьей и четвертой степеней. Жаль лишь, что слишком часто эти уравнения не решаются, так как полученные формулы приводят к нелепой операции извлечения квадратного корня из отрицательного числа.

Выступавший следующим алгебраист XVII в. написал формулу квадрата суммы уже в привычном для нас виде:

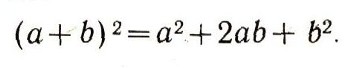
Он добавил, что его предшественники слишком узко понимают эту формулу. Прежде всего, в ней а и b

Рис. 1.

не обязательно являются длинами отрезков, а сами могут быть площадями, объемами, весами и даже отрицательными числами. Более того, вместо а и b можно подставить любые многочлены, например:

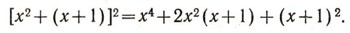
Он сказал еще, что эта формула является только одной из большого числа знакомых ему алгебраических формул и что ему хорошо известно искусство буквенных вычислений, а это искусство и есть алгебра.

Алгебраист XVIII в. заявил, что о формуле квадрата суммы нечего много говорить: эта формула, как и все буквенные вычисления, - удел школьной математики. При этом он отметил, что она всегда верна, и притом не только для положительных или отрицательных чисел, но и для комплексных, а эти числа совсем не такая уж нелепость! Что же касается предмета алгебраической науки, то это вовсе не искусство буквенных вычислений, а умение решать уравнения и системы уравнений. Для систем уравнений первой степени у него даже есть общая формула решения.

Выступление математика XIX в. часто прерывалось возгласами недоверия и шумными восклицаниями. Было ясно, что это выступление явилось для большинства участников полной неожиданностью. Да и в самом деле, выступавший заявил, что формула (a+b)² = a²+2ab + b² верна далеко не во всех случаях! Например, ирландский математик У. Гамильтон занимался обобщением комплексных чисел (так называемыми гиперкомплексными числами). Он построил числа, названные кватернионами, у которых не одна, а целые три мнимые единицы i, j, k. Так вот, для кватернионов (которые находят много интересных применений) формула квадрата суммы просто неверна. Неверна потому, что здесь мы сталкиваемся со случаем, когда умножение некоммутативно, т. е. не выполняется перемести-тельный закон умножения (например, ij = k, ji= -k), а при выводе формулы квадрата суммы мы пользуемся равенством ab = ba.

Выступавший сказал, что другие математики рассмотрели еще более удивительные обобщения комплексных чисел, для которых умножение не только некоммутативно, но даже и неассоциативно, т. е. в общем случае

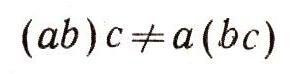
Выступивший вслед затем алгебраист XX в. сказал, что гиперкомплексные числа - это только примеры к тем общим теориям, которыми он занимается. Он может доказывать теоремы, которые верны не только для гиперкомплексных чисел одного вида, а для всех гиперкомплексных чисел (или для очень многих видов таких чисел). Он умеет складывать и умножать не только числа и многочлены, а и... квадратные таблицы, геометрические и алгебраические преобразования, логические суждения и т. д. (см. ст. "Алгебра множеств и алгебра логики").

- Как же вам удается оперировать с такими непохожими друг на друга вещами, как квадратные таблицы, гиперкомплексные числа, геометрические преобразования? Что может быть общего в действиях над ними? И как вы узнаете, какие формулы имеют место в тех или иных случаях?

- Весьма несложно; для этого в моем распоряжении имеется столь мощное оружие, как аксиоматический метод, который...

- Не может быть, - воскликнул окончательно выведенный из равновесия древний грек, - ведь аксиомы относятся к области геометрии?!

...Прервем на этом нашу конференцию и постараемся разобраться во всем сказанном.

перейти к началу страницы