Правила вывода

В заключение скажем еще несколько слов о правилах, связанных с употреблением символа =>. Установление того, что два высказывания а и b связаны соотношением

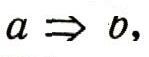
называется выводом; при этом высказывание а называется условием, а высказывание b - следствием. С выводами такого рода мы все время встречаемся в науке и в практической жизни, так, например, заключение любой теоремы является следствием ее условия. Правильность вывода обеспечивается соблюдением определенных правил логики. Эти правила логики могут быть обоснованы с помощью соотношений алгебры высказываний. Известное уже нам соотношение "Если

и b=>c, то a=>c"

читается так: "Если из а следует b и из b следует с, то из а следует с". Это соотношение используется в рассуждениях весьма часто. Например, поскольку теорема "Сумма углов треугольника равна 180°" вытекает из аксиомы параллельных линий, а теорема "Внешний угол треугольника равен сумме внутренних углов, не смежных с ним" вытекает из теоремы о сумме углов треугольника, можно также сказать, что теорема о внешнем угле треугольника является следствием аксиомы параллельных.

Соотношение "Если a=>b, to b=>a" читается так: "Если из высказывания а следует высказывание b, то из отрицания высказывания b вытекает отрицание высказывания а". Это обстоятельство лежит в основе весьма распространенного метода вывода (или доказательства) от противного. Пусть мы хотим доказать теорему (рис. 31): если соответственные углы АКМ и CLM, образованные прямыми АВ и CD с секущей MN, равны между собой (это есть утверждение а), то прямые АВ и CD параллельны (это есть утверждение 6). Вместо того чтобы доказывать соотношение a=>b

Рис. 31

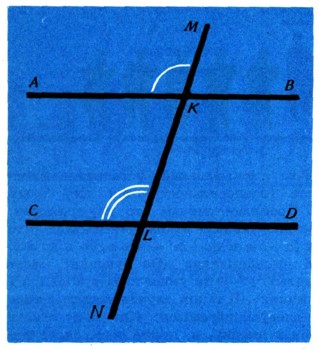
докажем, что b=>a, т. е. что из отрицания b вытекает отрицание а. Предположим, что прямые АВ и CD не параллельны, т. е. что они пересекаются в некоторой точке Р (рис. 32). В таком случае углы АКМ и CLM не будут равны (это внешний угол треугольника PKL и не смежный с ним внутренний угол). Таким образом, соотношение

Рис. 32

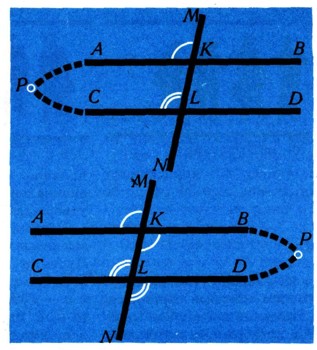
доказано, тем самым доказано и соотношение

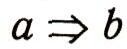
(строго говоря, здесь надо применить к соотношению b=>a рассматриваемое предложение алгебры логики и воспользоваться законом двойного отрицания: если

т. е. a=>b.

Уже эти примеры показывают ту большую роль, которую играют в любой научной теории правила алгебры логики. В последние годы роль этих правил особенно сильно возросла в сбязи с возникшей задачей передачи целого ряда операций, выполняющихся людьми, электронным вычислительным машинам. При этом оказалось необходимым научить машину правилам логики, т. е. тем правилам, которыми люди обычно пользуются, зачастую не отдавая себе полного отчета в существе этих правил. Но для того чтобы эти правила могли быть заложены в "электронную память" машины, необходимо четко сформулировать их. Эти четкие формулировки и доставляет нам математическая логика.

Рис. 33. Сложение и умножение множеств можно хорошо проиллюстрировать, используя геометрические фигуры разных цветов. В первой строке расположены фигуры, которые образуют универсальное (или единичное) множество. В других строках схемы из этого универсального множества I образованы новые множества А, В, С, D и их дополнения

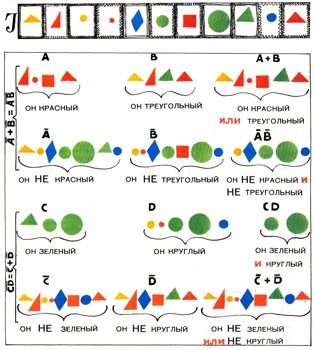
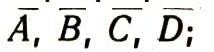
над этими множествами или их дополнениями произведены операции сложения и умножения.

перейти к началу страницы