Законы мысли

Теперь мы можем ответить на вопрос о том, почему сочинение Дж. Буля, в котором впервые строилась булева алгебра, посвящено выяснению "законов мысли". Дело в том, что правила алгебры высказываний есть те законы, которые играют руководящую роль в процессе нашего мышления.

Многие из этих законов в логике имеют специальные названия. Например, соотношение

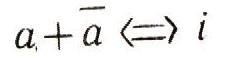
выражает так называемый закон исключенного третьего. Этот закон можно сформулировать так: сумма каждого утверждения и его отрицания тождественно истинна, другими словами, высказывание или его отрицание всегда истинно. Например, тождественно истинно утверждение "Он отличник или он не отличник". Другими словами, для каждого элемента универсального множества обязательно справедливо либо высказывание а, либо его отрицание а - третьего не дано. Соотношение

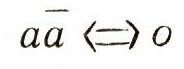
выражает закон противоречия. Согласно этому закону ни для одного объекта не может быть одновременно верно и утверждение а, и его отрицание а. Например, ни один ученик не может одновременно являться и отличником и неотличником. Но если выскдзывания а и а не могут быть истинны одновременно, то произведение аа тождественно ложно, т. е. множество истинности высказывания аа пусто. Соотношение

выражает хорошо известный закон двойного отрицания. Этот закон утверждает, что отрицание отрицания совпадает с исходным высказыванием. Так, отрицанием высказывания "Этот ученик - мальчик" является утверждение "Этот ученик - девочка", а двойное отрицание "Этот ученик не девочка" возвращает нас к первоначальному высказыванию "Этот ученик - мальчик".

Аналогичный характер имеют и все остальные правила алгебры высказываний, устанавливающие эквивалентность (равносильность) тех или -иных утверждений. Проиллюстрируем это на примерах.

Первый дистрибутивный закон утверждает, что высказывания (а + b)с и ас + bс - это одно и то же. Пусть а есть высказывание "Он (ученик) умеет играть в шахматы", b - "Он умеет играть в шашки" и с - "Он отличник". В таком случае высказывание (а + b)с имеет следующий смысл: "Он умеет играть в шахматы или в шашки, и, кроме того, он отличник", а высказывание ас + bс - смысл: "Он умеет играть в шахматы и является отличником либо он умеет играть в шашки и является отличником". Но ясно, что эти два высказывания по существу означают одно и то же.

Второй дистрибутивный закон означает, что эквивалентны два высказывания ab + c и (а + с)(b + с). Если высказывания а, b к с имеют тот же смысл, что и выше, то высказывание ab + C означает: "Он умеет играть в шашки и в шахматы или является отличником". Высказывание (а + с)(b + с) имеет следующий смысл: "Он умеет играть в шахматы или является отличником; одновременно с этим он умеет играть в шашки или является отличником". Но нетрудно понять, что последнее высказывание по существу совпадает с первым: ведь если ученик, о котором здесь идет речь, не является отличником, то он обязательно умеет играть и в шахматы и в шашки.

Наконец, остановимся еще на так называемых правилах де Моргана;

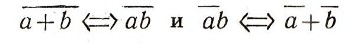
(они называются так по имени английского логика XIX в. А. де Моргана, впервые установившего эти правила). Пусть, например, а - это высказывание "Он умеет играть в шахматы", b - "Он умеет играть в шашки". В таком случае сложное высказывание а + b есть отрицание того, что ученик умеет играть в шахматы или в шашки. Но это отрицание, очевидно, эквивалентно утверждению о том, что ученик не умеет играть ни в шахматы, ни в шашки, т. е. высказыванию ab. Аналогично, отрицание утверждения о том, что ученик умеет играть и в шахматы и в шашки (т. е. высказывание ab), равносильно утверждению о том, что он не умеет играть в шахматы или не умеет играть в шашки; но это и есть высказывание а + b. .

перейти к началу страницы