Математика
Алгебра множеств и алгебра логики.
Дополнение множества. Аналогия между сложением и умножением множеств
Вернемся к установленным выше свойствам действий алгебры множеств. Сразу бросается в глаза чрезвычайно тесная связь между законами, относящимися к сложению множеств, и законами умножения. Выпишем снова эти законы:
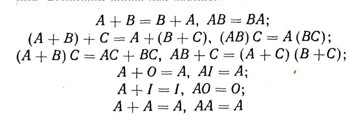
и т. д. Из этой таблицы видно, что всякое равенство, тождественно выполняющееся в алгебре множеств, при замене знака сложения множеств знаком умножения, и наоборот, и замене пустого множества О (если оно входит в наше равенство) универсальным множеством, и наоборот, переходит в новое равенство, также тождественно выполняющееся.
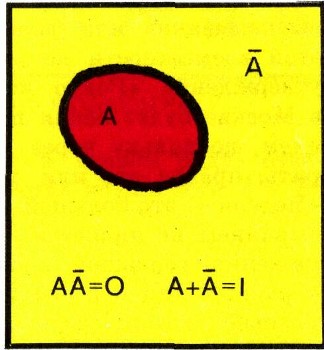
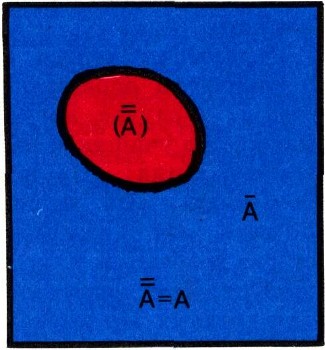
Сейчас мы докажем это утверждение в общем виде. Для этого нам понадобится одна своеобразная операция алгебры множеств, сопоставляющая новое множество не с двумя заданными множествами (подобно сумме А + В и произведению АВ заданных множеств), а с одним множеством A. Эта операция называется образованием дополнения и обозначается чертой, поставленной над множеством. А именно, через А (читается: "дополнение А") мы будем обозначать множество всех элементов универсального множества I, не принадлежащих множеству А. Так, если А есть множество отличников из нашего класса, то множество А состоит из всех учеников, не являющихся отличниками. На диаграмме множество А изображается частью квадрата I, не покрытой фигурой А (рис. 23). Ясно, что A+A=I, АА = О (см. тот же рис. 23, на котором графически изображены множества А я А); эти два равенства можно даже принять за определение множества А Отметим еще, что(A) = A (рис. 24). Это последнее равенство короче записывают так:
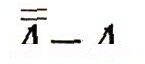
Очевидно, что I = О и O = I (так как все элементы входят в универсальное множество I и ни один элемент не входит в пустое множество О). Кроме того, легко видеть, что если
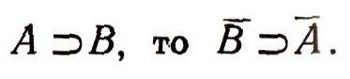
т. е. если множество В составляет часть множества А, то дополнение А составляет часть дополнения В (рис. 25 а, 25 б). Докажем теперь следующие два важных соотношения :
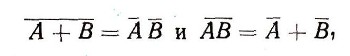

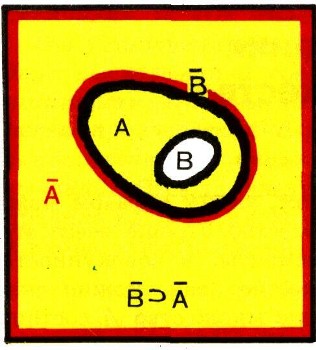
или словами: дополнение суммы двух множеств совпадает с пересечением дополнений этих множеств; дополнение произведения двух множеств совпадает с суммой дополнений этих множеств. В самом деле, на рис. 26 а закрашены множества А и В, а на рис. 26 б, 26 в - их дополнения Л и В. Но ясно, что фигура, закрашенная зеленым цветом на рис. 26 а, является дополнением до всего квадрата I фигуры, закрашенной на обоих рис. 26 б и 26 в, т. е. фигуры АВ; это и доказывает равенство
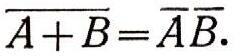

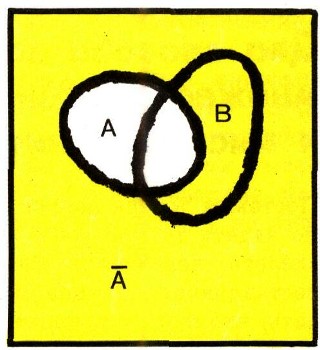
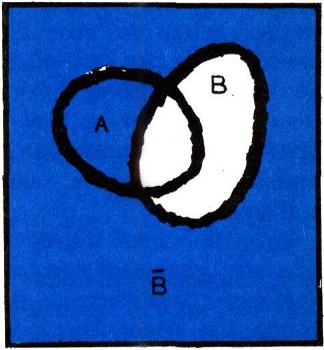
Аналогично, фигура, помеченная желтым на рис. 26 а, дополняет до всего квадрата фигуру, закрашенную на рис. 26 б или 26в, откуда следует, что АВ = А + В.
Из доказанных соотношений нетрудно вывести наше утверждение, позволяющее по каждому соотношению алгебры множеств построить новое соотношение. Рассмотрим какое угодно тождество алгебры множеств, например первый дистрибутивный закон: (А + В)С = АС + ВС.
Так как множества (А+В)С и АС + ВС совпадают, то совпадают и дополнения этих множеств:
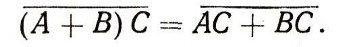
Но мы знаем, что
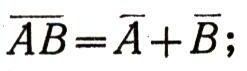
поэтому
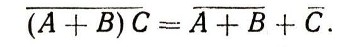
С другой стороны, нам известно, что
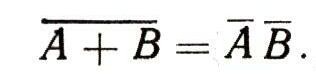
Таким образом,
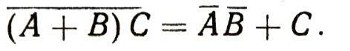
Далее, в силу того же закона
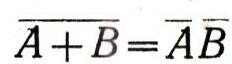
алгебры множеств, имеем:
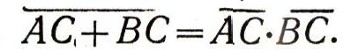
Но
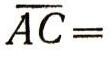
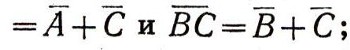
поэтому
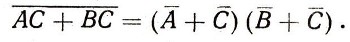
Таким образом, мы приходим к равенству:
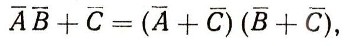
которое, очевидно, лишь по форме отличается от второго дистрибутивного закона:
АВ + С = (А + С) * (В + С),
(вместо самих множеств А, В и С в нашем равенстве выступают их дополнения
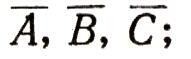
но это совершенно несущественно, поскольку как сами рассматриваемые множества, так и их дополнения произвольны). Таким образом, с помощью образования дополнения мы вывели из первого дистрибутивного закона второй дистрибутивный закон.
Точно таким же путем можно из любого тождества алгебры множеств получить другое тождество, в котором всюду операция сложения заменена умножением, и наоборот. При этом если в первоначальное тождество входили множества О и I, то в новом тождестве они заменяются соответственно на I и О; это связано с тем, что
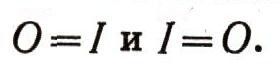
2i.SU ©® 2015