Алгебра множеств

Рассмотрим систему всевозможных множеств (совокупностей) тех или иных объектов; например, будем говорить о множествах учеников класса.

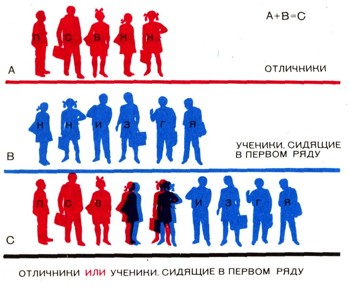
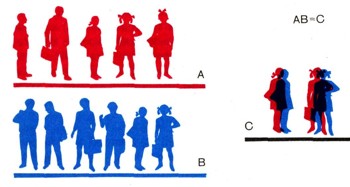
Сумму А + В двух множеств А и В определим как такое множество, которое получается при объединении множеств А к В; другими словами, в множество А + В входят все те, и только те, объекты, которые входят в множество А или в множество В. Так, например, если А есть множество отличников нашего класса, состоящее из учеников Пети, Саши, Веры, Кати и Наташи, а В - множество учеников, которые сидят в первом ряду, состоящее из школьников Илюши, Гриши, Зои, Кати, Наташи и Яши, то сумма А + В этих двух множеств состоит из учеников, которые являются отличниками или сидят в первом ряду; в нее входят ученики Петя, Саша, Вера, Катя, Наташа, Илюша, Гриша, Зоя и Яша (рис. 3).

Рис. 3

То обстоятельство, что мы назвали сложением совершенно новую операцию, не должно нас смущать, ведь мы и раньше каждый раз, когда переходили от чисел одной природы к числам другой природы, определяли сложение по-новому. Ясно, например, что сложение положительных и отрицательных чисел - это не то же самое, что сложение одних положительных чисел; так, сумма чисел 5 и (- 3) -это то же самое, что разность чисел 5 и 3. Сложение дробей не то же самое, что сложение целых чисел; рис. 1, изображающий сложение чисел, становится непригоден, когда речь заходит о дробях. Однако, называя уже знакомым нам словом "сложение" новую операцию, мы каждый раз должны были лишь "доучиваться", но не "переучиваться"-навыки, выработавшиеся в процессе действий с натуральными числами (и нулем), оказываются полезными и при действиях с дробями, правила действий над положительными числами полезны и при действиях с относительными' (положительными или неположительными!) числами и т. д. Это связано с тем, что общие законы, которым подчиняется операция сложения целых чисел, остаются в силе и в дальнейшем, скажем при переходе к дробным числам; так, например, в обоих случаях сложение коммутативно (a + b = b + a) и ассоциативно [(a.+ b) + c = a+(b + c)].

Рис. 4

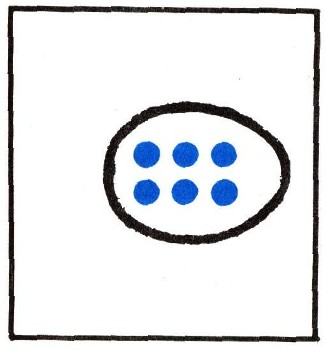
Посмотрим теперь, сохраняют ли силу эти законы и для множеств. При этом нам удобно будет использовать специальные диаграммы, иллюстрирующие действия над множествами. Условимся обозначать весь класс (точнее говоря, множество всех учеников класса) квадратом; в этом квадрате можно расставить ряд точек, по числу учеников (рис. 4). При этом отдельные множества учеников будут изображаться частями квадрата: так, например, изображенная на рис. 5а фигура графически иллюстрирует множество А отличников, а изображенная на рис. 5б - множество В учеников, сидящих в первом ряду. Под суммой двух множеств Л и В понимается фигура, получаемая объединением фигур, изображающих множества А и В (рис. 6).

Рис. 5а

Рис. 5б

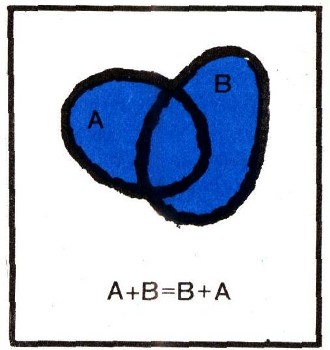
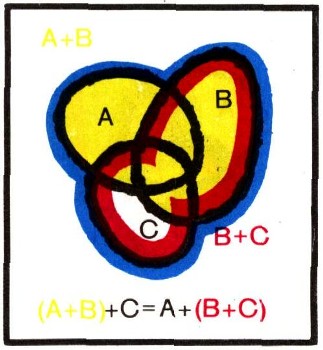
Такие диаграммы принято называть диаграммами Эйлера или диаграммами Венна (по имени английского логика Дж. Венна, 1834-1923). Они позволяют наглядно представить операцию сложения множеств и проверить ее свойства. Ясно, например, что А+В=В+А (коммутативный закон для сложения множеств; рис. 7). Также ясно, что (А + В)+С=А+(В + С) (ассоциативный закон для сложения множеств; рис. 8). Сумму (A + B)+C=A+(B + C) естественно обозначать просто через А+В + С (без скобок).

Рис. 6 Сумма двух фигур - это их объединение.

Рис. 7

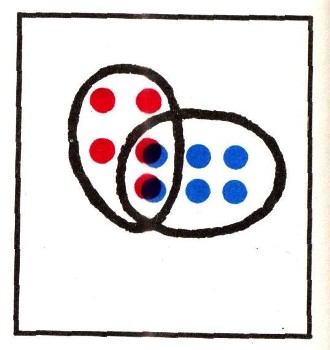
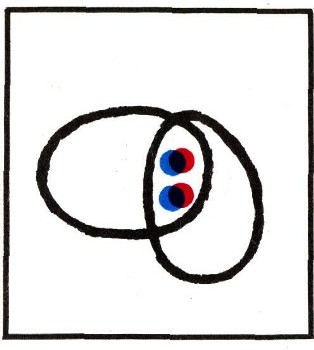
Определим теперь произведение А * В, или АВ, двух множеств А и В как множество, получаемое в пересечении множеств А и В; другими словами, в множество АВ входят те, и только те, элементы, которые входят как в множество А, так и в множество В. Так, например, если А и В - указанные выше множество отличников и множество учеников, сидящих в классе в первом ряду, то множество АВ состоит из тех учеников, которые являются отличниками и сидят в первом ряду; оно состоит всего из двух учеников - Кати и Наташи (рис. 9). На рис. 10 то же множество АВ изображено на диаграмме как пересечение множеств А и В.

Рис. 8

Рис. 9

Рис. 10. Произведение двух фигур - это их пересечение.

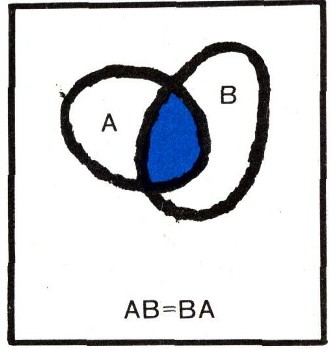
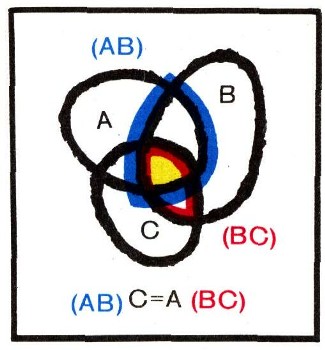
Использование термина "произведение" в совершенно новом смысле оправдывается тем обстоятельством, что, как и для обыкновенного умножения, мы имеем: АВ = ВА (коммутативный закон для умножения множеств; рис. 11) и (АВ)С = А(ВС) (ассоциативный закон для умножения множеств; рис. 12). Множество (АВ)С = А(ВС) естественно обозначать просто через ABC (без скобок).

Рис. 11

Рис. 12

Рис. 13а

Рис. 13б

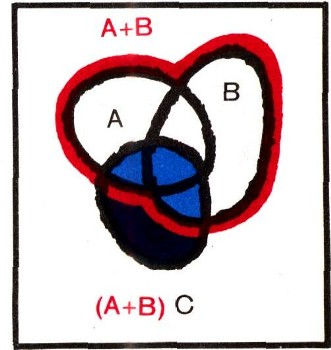
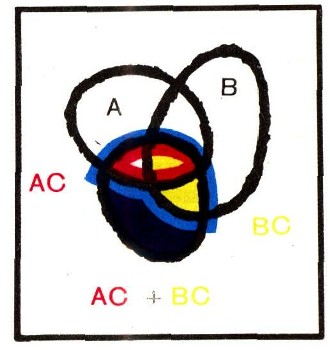
Проверим теперь, выполняется ли для множеств дистрибутивный закон. На рис. 13а выделены множества А + В и С, синим цветом отмечено их произведение - множество (А + В)С. На рис. 136 красным и желтым цветом обозначены множества АС и ВС, асиним цветом - их сумма,, т. е. множество АС + ВС. Но легко видеть, что множество, закрашенное синим цветом на рис. 13а, - это в точности то множество, которое отмечено синим цветом на рис. 13б. Отсюда заключаем: в "алгебре множеств" выполняется дистрибутивный закон:

(А + В)С=АС+ВС

перейти к началу страницы