Мощность множества

Нам нужно осмыслить полученный результат и подвести некоторые итоги всему до сих пор сказанному. Мы начали с понятия взаимно однозначного соответствия между двумя множествами, возможность которого (в случае конечных множеств) равносильна тому, что оба множества состоят из одного и того же числа элементов. Это обстоятельство указывает путь

и к установлению количественного равенства, или количественной эквивалентности, между двумя бесконечными множествами. Мы скажем, что два (конечных или бесконечных) множества количественно эквивалентны, или имеют одну и ту же мощность, если между ними возможно установить взаимно однозначное соответствие. Понятие "одинаковая мощность" означает для конечных множеств, что они состоят из одного и того же числа элементов. Далее скажем, что множество А имеет большую мощность, чем множество В, если можно множество В отобразить взаимно однозначно на часть множества Л и в то же время нельзя отобразить множество А на часть множества В. Теперь можем сказать, что счетные множества - это множества, количественно эквивалентные множеству натуральных чисел. Но существуют множества и несчетные, например множество всех действительных чисел, интервала (0; 1) и любого другого интервала. Всякий интервал числовой прямой может быть взаимно однозначно отображен на интервал (0; 1). (Докажите это!)

Для того чтобы убедиться в том, что всякое несчетное множество имеет большую мощность, чем каждое счетное множество (все счетные множества имеют, очевидно, одну и ту же мощность), надо доказать следующие два предложения:

1. Всякое подмножество счетного множества или конечно, или счетно.

2. Всякое бесконечное (значит, в частности, всякое несчетное) множество содержит счетное.

Доказательство первого утверждения. Пусть X -счетное множество, X₀ - какое-нибудь подмножество (т. е. часть) множества X. Элементы множества X могут быть занумерованы посредством натуральных чисел, т. е. записаны в виде:

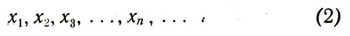
Среди этих элементов содержатся и все элементы множества Х₀. Пусть это будут - в порядке возрастания номеров в последовательности (2) - элементы :

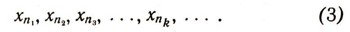
Возможно одно из двух: или последовательность (3) обрывается на каком-то конечном шаге k, т. е. множество X₀ состоит Из конечного числа элементов: Xn₁„ Xn₂, ..., Xn_k, или же мы имеем бесконечную последовательность:Xn₁, Xn₂, ..., Xn_k, ..., которую можем переписать, полагая y₁ = х_п1, у₂ = х_n2, ... , y_k = x_nk .. ., в виде

y₁, y₂, ..., y_n, ...

непосредственно показывающем, что Х₀ - счетное множество.

Доказательство второго утверждения. Путь X -бесконечное множество. Выбираем в X какой-нибудь элемент х₁. Несомненно, в X имеются элементы, отличные от х₁ (иначе X состояло бы из одного элемента и было бы конечным). Возьмем один из таких элементов и обозначим его через Х₂- Элементы х₁ и x₂ не исчерпывают множества X, поэтому существует элемент x₃ множества X, отличный как от х₁, так и от х₂. И так далее. Продолжая этот процесс, получим счетное множество: х₁, x₂, x₃, ... , х_п, ... содержащееся в Х.

Итак, на вопрос, поставленный в начале нашего изложения: "Существуют ли бесконечные множества разных "степеней бесконечности" (т. е. разных мощностей)?" - мы можем ответить утвердительно. Существуют состоящие из действительных чисел множества по крайней мере двух различных мощностей: множество всех действительных чисел какого-нибудь интервала, с одной стороны, и любое счетное множество действительных чисел (например, множество положительных рациональных чисел) - с другой. К этому выводу мы пришли, обосновывая количественную оценку бесконечных множеств при помощи понятия взаимно однозначного соответствия. Однако не следует думать, что взаимно однозначное соответствие между бесконечными множествами во всем похоже на взаимно однозначное соответствие между множествами конечными.

Очевидно, никакое конечное множество нельзя взаимно однозначно отобразить на его часть (часть никогда не равна целому). Уже простейшие примеры показывают, что это утверждение решительно перестает быть верным в области бесконечных множеств: мы видели, что всякое бесконечное подмножество счетного множества счетно, т. е. счетное множество может быть взаимно однозначно отображено на всякую его бесконечную часть. Например, подписывая под всеми натуральными числами подряд все четные:

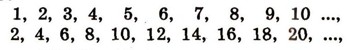
получим взаимно однозначное соответствие между множеством всех натуральных чисел и его частью -множеством одних лишь четных чисел. Другой пример. Существует взаимно однозначное отображение между множеством всех действительных чисел (между всей числовой прямой) и любым его интервалом. Для того чтобы получить такое соответствие, можно поступить так. Построим в плоскости окружность, касающуюся оси абсцисс, и возьмем нижнюю полуокружность PQ этой окружности (рис. 4). Концы Р и Q полуокружности к ней не причисляются. Установим взаимно однозначное соответствие между всеми точками полуокружности PQ и всеми точками числовой прямой. Для этого сначала поставим в соответствие каждой точке e прямой ту точку n полуокружности, в которой ее пересекает луч, идущий из центра окружности в точку e.

Рис. 4.

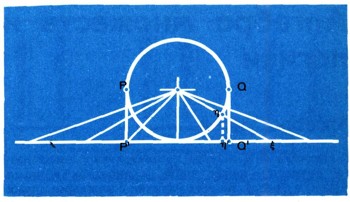
Теперь спроектируем полуокружность PQ на интервал P'Q' оси абсцисс и поставим в соответствие точке n полуокружности ее проекцию n'. В результате каждой точке e прямой оказалась поставленной в соответствие точка n интервала P'Q', и полученное соответствие есть взаимно однозначное отображение всей числовой прямой на интервал P'Q'.

Можно доказать и другие, кажущиеся на первый взгляд парадоксальными, теоремы о мощности различных множеств. Упомянем лишь одну из них: Существует взаимно однозначное соответствие между всеми точками прямой и всеми точками плоскости.

Заметим, наконец, следующее. В математике наибольшее значение имеют так называемые числовые множества, т. е. множества, элементами которых являются действительные числа. Все известные в настоящее время числовые множества или счетны, или имеют ту же мощность, что и вся числовая прямая. Возникла, таким образом, гипотеза, что всякое несчетное числовое множество имеет ту же мощность, что и вся числовая прямая. Эта гипотеза была высказана еще Кантором и известна под названием континуум-гипотезы. Трудности, связанные с континуум-гипотезой, получают свое освещение в так называемой математической логике, и мы о них здесь говорить не можем.

Эта статья имеет своей целью дать лишь начальное представление о некоторых простейших понятиях обширной области математики - теории множеств, области, возникшей менее чем сто лет назад.

Решение к стр. 354. Построим ряд параллельных отрезков, промежутки между которыми будем считать изображением секунд. Точками изобразим удары боя первых (А) и вторых (В) часов соответственно условию задачи (см. рис. справа).

Схема показывает, что под номерами 5, 11, 17 удары происходят одновременно и на слух сливаются каждый раз в один удар. Максимальное число ударов для каждых часов в отдельности равно 12, но если бы это было так, то мы насчитали бы 21 удар. На схеме изображены 19 ударов, что соответствует 11 раздельным ударам часов А и В. Значит, часы показывали 11.

Ну и дроби!

Беру две дроби, каждую возвожу в квадрат, результаты складываю, получаю некоторое число S. Теперь каждую из первоначальных дробей возвожу в куб, результаты складываю и... получаю то же самое число S. Выходит, что сумма квадратов двух чисел равна сумме кубов тех же чисел. Такое заключение кажется неправдоподобным. И все же это не фокус, не трюк. Есть много пар таких дробей. Попробуйте найти их.

Кто сильнее!

Борис взялся за один конец каната, а Аркадий и Николай вместе - за другой. Перетянул Борис, хотя и с большим трудом. Когда с одной стороны встали Борис и Аркадий, а с другой Владимир с Николаем, то ни та ни другая пара не смогла перетянуть канат на свою сторону. Но стоило только Николаю и Аркадию поменяться местами, как победу одержала пара Владимир и Аркадий. По нашему убеждению, основанному на точных рассуждениях, самый сильный из этих четырех друзей - Владимир, следующий по силе - Борис, а на последнем, четвертом месте - Николай. Тот из читателей, кто согласен с нашим заключением, должен уметь обосновать его.

перейти к началу страницы