Счетные множества

Вообще, если все элементы какого-нибудь множества X удается занумеровать посредством натуральных чисел так, что каждое натуральное число придано в качестве номера лишь одному элементу множества X, то такой нумерацией устанавливается взаимно однозначное соответствие между данным множеством X и множеством всех натуральных чисел. И обратно, всякое взаимно однозначное соответствие между каким-нибудь множеством X и множеством всех натуральных чисел можно рассматривать как нумерацию (сосчитывание) элементов множества X посредством натуральных чисел - мы просто приписываем каждому элементу множества X в качестве номера соответствующее ему натуральное число.

Мы здесь коснулись очень важного понятия. Ведь установление взаимно однозначного соответствия между некоторым множеством X и множеством всех натуральных чисел есть прямое перенесение в область бесконечных множеств пересчитывания какого-либо конечного множества (например, корзины яблок или стада гусей) с помощью натуральных чисел. Только в случае конечных множеств мы для сосчитывания его элементов нуждаемся лишь в конечном числе чисел (мы считаем: раз, два, три и т. д. - до того числа, которое показывает, сколько у нас яблок в корзине или гусей в стаде). В примере множества треугольников

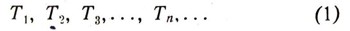
или вообще любого множества X, которое может быть приведено во взаимно однозначное соответствие с множеством всех натуральных чисел, мы вынуждены в качестве номеров воспользоваться всеми натуральными числами. Но теперь возникает самый главный, реновной для всей теории множеств вопрос. Всегда ли можно занумеровать элементы бесконечного множества натуральными числами так, чтобы каждый элемент данного множества получил определенный номер? Другими сяовами: можно ли установить взаимно однозначное соответствие между произвольным бесконечным множеством и множеством всех натуральных чисел?

Оказывается, ответ на этот вопрос отрицательный, и мы постараемся убедиться в этом. Но сначала несколько подготовимся. Прежде всего установим название для тех множеств, которые могут быть поставлены во взаимно однозначное соответствие с множеством всех натуральных чисел. Эти множества называются счетными. Это название естественно: счетное множество - это такое множество, которое может быть сосчитано посредством натуральных чисел. Наша задача - показать, что существуют несчетные множества, т. е. такие, которые не могут быть поставлены во взаимно однозначное соответствие с множеством всех натуральных чисел.

перейти к началу страницы