Множества конечные и бесконечные

Обычно арифметику определяют как науку о числах. Числа в простейшем смысле слова, т. е. так называемые натуральные числа: 1, 2, 3, 4, 5, ..., отвечают на вопрос "сколько?". Сколько учеников в классе? Сколько книг на столе? Сколько гусей на пруду?

Но каждый раз, когда мы спрашиваем: "Сколько предметов?", мы должны иметь эти предметы, их совокупность. Вот мы и говорим о совокупности всех учеников, образующих данный класс, о совокупности книг, лежащих на столе, о совокупности гусей, плавающих на пруду.

Каждое натуральное число есть число предметов (одушевленных или неодушевленных), образующих некоторую совокупность. Иногда эти предметы легко сосчитать, например когда идет речь о числе книг, лежащих на столе, или о числе учеников, сидящих в классе.

Но значительно труднее ответить на вопрос, сколько в данный момент плавает китов в Мировом океане или даже сколько зайцев живет в подмосковных лесах. И уж совсем трудно точно сказать, сколько молекул в стакане воды или звезд в нашей Галактике.

Однако во всех этих случаях мы уверены, что число это конечное, хотя, может быть, и очень большое и недоступное для точного вычисления при данном состоянии наших научных познаний.

В математике рассматриваются не только конечные, но и бесконечные совокупности. Простейшим примером такой совокупности является совокупность, ' или, как принято говорить, множество, всех натуральных чисел: 1, 2, 3, 4, 5, ....

Мы уже сказали, что каждое натуральное число есть число предметов, образующих ту или иную совокупность, то или иное множество. Но множество всех натуральных чисел уже не есть конечное множество. На вопрос: "Сколько всего натуральных чисел?" - приходится ответить, что их бесконечно много. Какое бы большое число натуральных чисел мы ни задумали, всегда есть такие натуральные числа, которые не вошли в число задуманных.

В математике мы постоянно сталкиваемся с примерами бесконечных множеств. Возьмем, например, равносторонний треугольник Т₁, впишем в него равносторонний треугольник Т₂. Вершины треугольника Т₂ суть середины сторон треугольника Т₁. Таким же образом впишем в Т₂ равносторонний треугольник Т₃ в Т₃ впишем T₄ и т. д. (рис. 1). Это построение приводит к бесконечному множеству равносторонних треугольников: T₁, Т₂, Т₃, T₄, T₅, .... T_n... . (1)

Рис. 1.

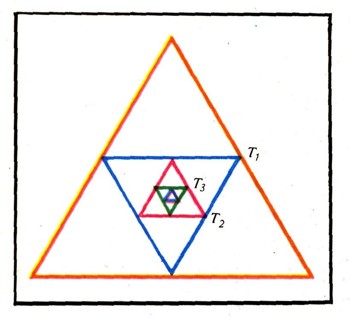
Тем более бесконечным является множество всех вообще равносторонних треугольников, лежащих в данной плоскости.

Последняя фраза несколько двусмысленна: слово "более" может быть воспринято в ней как составная часть выражения "тем более", употребленного в смысле "и подавно". Раз есть уже бесконечное множество равносторонних треугольников, получающихся при некотором определенном построении, то и подавно множество всех равносторонних треугольников бесконечно.

Но слово "более" может быть понято и как сравнительная степень прилагательного, и тогда высказанное выше суждение означает, что множество всех равносторонних треугольников, лежащих в данной плоскости, в каком-то смысле является "более бесконечным", чем бесконечное множество построенных нами треугольников: T₁, Т₂, Т₃, .... T_n... . . . . .

Как видите, мы затронули интересный вопрос, долгое время отпугивавший ученых своей (впрочем, лишь кажущейся) парадоксальностью: существуют ли, если можно так выразиться, различные "степени" бесконечности? Возможна ли количественная оценка бесконечных множеств, позволяющая утверждать, что одно из двух бесконечных множеств является "более бесконечным", чем другое? Или же утверждение, что данное множество является бесконечным, окончательно в том смысле, что не дает возможности дальнейших различений или градаций количественного характера?

Первым, кто пытался ответить на этот вопрос, был знаменитый чешский математик и философ В. Больцано (1-я половина XIX в.), но он не смог полностью преодолеть все трудности, которые при этом возникли. Постараемся разобраться, в чем эти трудности и каково решение поставленного вопроса.

Бернард Больцано.

перейти к началу страницы