Математика
Интеграл и производная
Уравнение гармонических колебаний
Во многих случаях тела совершают колебания около положения равновесия под действием силы, величина которой пропорциональна отклонению тела от положения равновесия и которая стремится возвратить это тело в положение равновесия. Например, это имеет место для груза, подвешенного на пружине. Иначе говоря, сила, действующая на тело, выражается формулой:
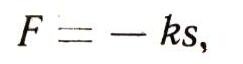
где s - отклонение тела от положения равновесия, a k - жесткость пружины. Поэтому (в силу второго закона Ньютона) дифференциальное уравнение движения тела имеет такой вид:

Обозначив положительное число k/m через w2, мы сможем записать это уравнение в виде:

Это уравнение называется уравнением гармонических колебаний, так как функция
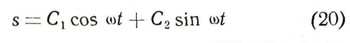
при любых С1 и С2 является решением этого уравнения. В самом деле, по формулам (13) и (14) скорость тела, движущегося по закону (20), равна:
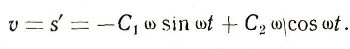
Продифференцировав еще раз, найдем ускорение:
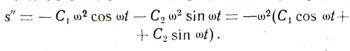
Но выражение, стоящее в скобках, равно s. Таким образом, взятая функция 5 действительно удовлетворяет уравнению s"=-w2s. Можно доказать, что всякое решение этого уравнения имеет такой вид.
Итак, сила, пропорциональная отклонению тела от положения равновесия и стремящаяся вернуть его в это положение, вызывает гармонические колебания частоты to, где w2 = k/m (т - масса тела, k - коэффициент пропорциональности).
Для колебаний электрической цепи можно также записать аналогичный закон, только надо заменить массу тела самоиндукцией катушки, путь, пройденный телом, - напряжением на конденсаторе, а скорость тела - током. Поскольку законы, управляющие этими явлениями, совершенно аналогичны, то и колебания, возникающие в обоих случаях, записываются одними и теми же формулами. А затухающие колебания возникают, если кроме силы, стремящейся вернуть тело в положение равновесия, действует еще сопротивление среды, пропорциональное скорости движения тела (или сопротивление электрической цепи).
2i.SU ©® 2015