Леверье и Адаме открывают новую планету

По второму закону Ньютона сила равна произведению массы на ускорение:

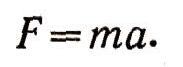
Но ускорение тела, движущегося прямолинейно, представляет собой скорость изменения скорости, т. е. является производной от скорости: a = v'. Сама же скорость является производной от пройденного пути: v = s'. Таким образом, чтобы найти ускорение движущегося тела, надо два раза продифференцировать функцию s(t). Поэтому ускорение называют второй производной от пути по времени. Обозначают это так:

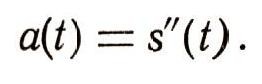
Пользуясь этим обозначением, мы можем записать второй закон Ньютона в следующем виде:

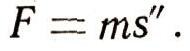
Сила F зависит от многих обстоятельств: от времени, от скорости движения, от того, в какой точке пространства находится движущееся тело. Например, на парашютиста, спускающегося с раскрытым парашютом, действуют сила тяжести mg и сила сопротивления воздуха, которую можно считать пропорциональной скорости падения, т. е. равной -kv. Таким образом, общая сила, Действующая на парашютиста, равна:

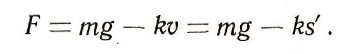
Следовательно, движение парашютиста описывается дифференциальным уравнением:

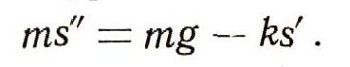
Иной вид имеет уравнение движения ракеты, вертикально поднимающейся по инерции после полного сгорания горючего. Сила притяжения ракеты к Земле обратно пропорциональна квадрату расстояния ракеты от центра Земли, т. е.

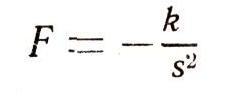
(мы считаем, что ракета вышла из земной атмосферы и потому на нее не действует сила сопротивления воздуха). Таким образом, указанное движение ракеты описывается дифференциальным уравнением:

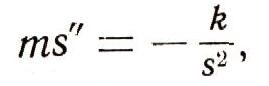
где m - масса ракеты. (Этим уравнением описывается также вертикальное падение метеорита на Землю до вхождения его в атмосферу.)

Вообще второй закон Ньютона позволяет описывать самые разнообразные движения тел с помощью дифференциальных уравнений. Можно написать дифференциальные уравнения для движения поршня паровой машины, корабля в море, планеты вокруг Солнца, искусственного спутника вокруг Земли.

Решая дифференциальные уравнения движения планет и их спутников (эти уравнения весьма сложны, так как планеты притягиваются не только к Солнцу, но и друг к другу), ученые предсказывают их будущее движение, узнают моменты солнечных и лунных затмений. Когда однажды оказалось, что планета Уран отклоняется от заранее вычисленной орбиты, ученые нисколько не усомнились в "правильности" математики. В середине XIX в. французский астроном У. Леверье и английский астроном Дж. Адаме одновременно и независимо один от другого сделали смелое предположение, что отклонение Урана вызывается притяжением новой, до тех пор неизвестной планеты. С помощью дифференциальных уравнений они высчитали положение этой новой планеты и указали, где нужно ее искать на небе. Точно в указанном месте эта планета (ее назвали Нептуном) была затем обнаружена.

Развлечение с числами

В последовательности натуральных чисел зачеркните простое число р и все кратные ему. Из оставшихся чисел образуйте такую последовательность: единица, сумма первых двух чисел, сумма первых трех чисел и т. д. В получившейся последовательности снова зачеркните числа, кратные р, и опять образуйте последовательность сумм таким же способом, как первый раз. Если указанную операцию выполнить р раз, причем в последний раз уже не производить никаких вычеркиваний, то образовавшиеся числа будут р-ми степенями натуральных чисел.

Пример, Пусть p = 3. Тогда из последовательности натуральных чисел надо вычеркнуть числа 3, 6, 9, 12,...; из оставшейся последовательности 1, 2, 4, 5, 7, 8, 10, 11,... образуем новую последовательность, как указано: 1, 3, 7, 12, 19, 27, 37, 48,...; вычеркивая числа, кратные 3, составляем третью последовательность: 1, 8, 27, 64,..., а это и есть последовательность кубов чисел натурального ряда: 1³, 2³, З³, 4³,..., как и было обещано!

Игра с кубами чисел

У каждого участника игры должна быть таблица кубов. Назначаем какое-нибудь целое число и ставим задачу: представить это число как алгебраическую сумму, пяти кубов.

Пусть назначено, например, число 1. Рассматриваем таблицу кубов и подбираем: 1 = 4³-3³-3³-2³-1³ или 1"=6³-5³-4³-3³ + 1³.

Цель игры: за отведенный промежуток времени подобрать как можно больше решений задачи. У вас, очевидно, возникнет такой вопрос: "Разве любое целое число может быть представлено в виде алгебраической суммы пяти кубов натуральных чисел, да еще несколькими способами?" Да, любое, и даже бесконечным числом способов. Это доказал польский математик В. Серпинский.

перейти к началу страницы