Математика

Содержание раздела

Интеграл и производная

Производная показательной функции

Теперь продифференцируем показательную функцию у = е^х. Мы уже знаем (см. статью "Функции в природе и технике"), что касательная к кривой у = е^х, проведенная в точке пересечения ее с осью ординат, наклонена к осям под углом 45°. Вспоминая геометрический смысл производной (см. стр. 343), мы можем сказать, что производная функции у = е^х в точке х = 0 равна tg45°, т. е. 1. Итак, (е^х)' | _{при х=о} =1

Чтобы вычислить производную функцию у = е^х в какой-либо точке х₀, сдвинем график этой функции на отрезок x₀. После сдвига в точке х ордината станет равной не е^х, а е^х-х0 , т. е. сдвинутая кривая является графиком функции у = е^х-х0 (рис. 33). При сдвиге графика касательная, проведенная к кривой у = е^х в точке x = 0, перейдет в касательную, проведенную к сдвинутой кривой (т. е. кривой у = е^х-x0) в точке х=х₀ (рис. 34).

 

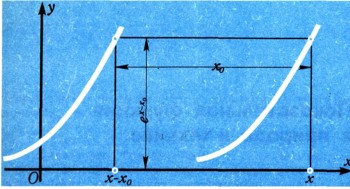
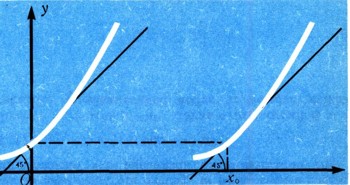
Таким образом, касательная к кривой у = е^х-x0 в точке x₀ наклонена к оси х под углом 45°, т. е.

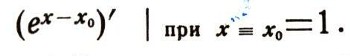
Теперь легко найти производную функции у = е^х в точке X=X₀. В самом деле, так как постоянный множитель е^x0 можно вынести за знак производной, получим:

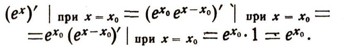
Этим доказано, что производная от функции е^х в точке X = X₀ равна е^х0 • Так как x₀- произвольная точка, то мы можем просто написать:

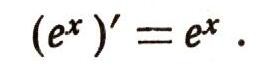
С помощью несложных рассуждений можно вывести следующую формулу:

 

перейти к началу страницы