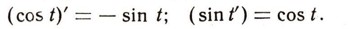Производные синуса и косинуса

Производные от тригонометрических функций проще всего вычислить исходя из физических соображений. Рассмотрим точку А, движущуюся по окружности радиуса R со скоростью wR. Будем считать, что при t = 0 точка А находилась в положении АО (рис. 31).

Рис. 31

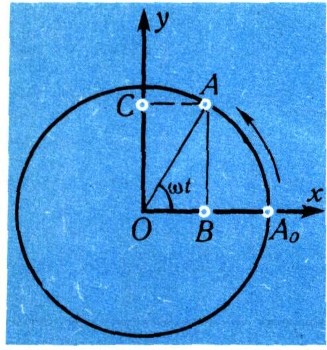
Через t секунд точка пройдет путь длиной wRt и окажется в положении А. Дуга А₀А имеет длину wRt, т. е. содержит wt радианов, значит, и угол АОА₀ равен wt радианам. Поэтому координаты точки А равны x = R cos wt и у = R sin wt (это легко выводится из треугольника АВО). Иными словами, проекция В точки А на ось Ох движется по закону x = R cos wt, а проекция С этой же точки на ось Оу движется по закону y = R sin wt. Найдем скорости этих колебаний.

Для этого разложим.скорость движения точки А на две составляющие: горизонтальную и вертикальную. Вектор скорости точки А (имеющий длину wR) направлен по касательной к окружности, проведенной в точке А, и потому образует с осью Ох угол wt + Пи/2. а с осью Оу - угол wt. Следовательно, его проекция на ось Ох (т. е. скорость движения точки В) равна:

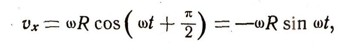
а его проекция на ось Оу (т. е. скорость движения точки С) равна:

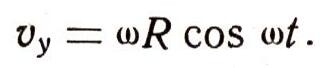
Мы доказали, что скорость колебания, происходящего по закону x=R cos wt, равна: v_x = - wR sin wt. Так как скорость является производной от пути по времени, это означает, что

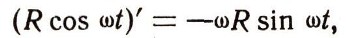
или при R = 1

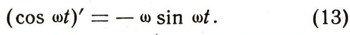
Точно так же доказывается (из рассмотрения движения точки С), что

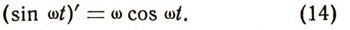
В частности, при w = 1 получаем:

перейти к началу страницы