Балка наибольшей прочности

Основным элементом любой строительной конструкции является балка. Прочность балки зависит от того, какую форму имеет ее поперечное сечение. Инженерные расчеты показывают, что прочность балки с прямоугольным сечением пропорциональна ширине балки а и квадрату ее высоты h. Иными словами, прочность такой балки (измеренная в некоторых единицах) равна kah², где k - коэффициент, зависящий от длины балки, материала, из которого она сделана, и т. д.

Рис. 28.

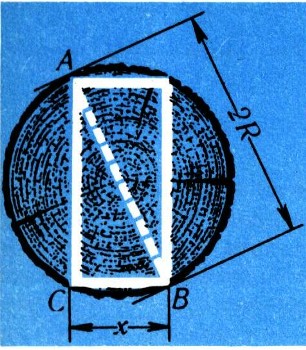
Деревянные балки приходится обычно вытесывать из круглых бревен. В связи с этим возникает задача, как из бревна, имеющего радиус R, сделать балку наибольшей прочности. На рис. 28 изображено поперечное сечение бревна. Разумеется, прочность вырезанной балки будет функцией от ширины этой балки. По если взять ширину слишком большой (почти равной диаметру бревна), то получится балка очень маленькой высоты и прочность ее будет мала (рис. 29, а). Мала будет прочность балки, если сделать ее слишком узкой (рис. 29, б). Чтобы найти, при каком соотношении длины и ширины прочность будет наибольшей, выразим прочность балки как функцию от ее ширины х. Из треугольника ABC, изображенного на рис. 28, видно, что высота балки, имеющей ширину х, равна

Рис. 29.

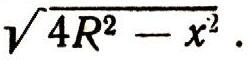
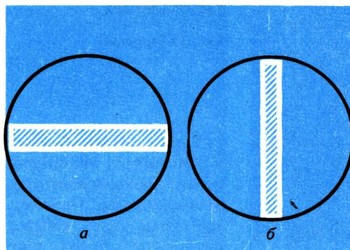
Поэтому прочность такой балки равна:

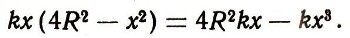
График функции y = 4R²kx - kx³ имеет вид, указанный на рис. 30, а ее производная равна 4R²k - 3kx²и обращается в нуль при

Рис. 30.

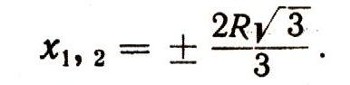
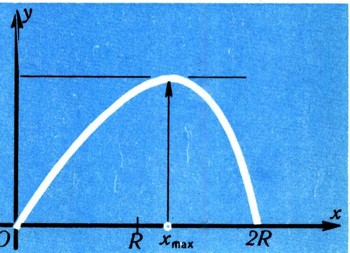
Поскольку ширина балки должна быть положительной, получаем, что самая прочная балка будет, если ширина ее по формуле:

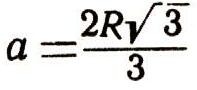
высота балки определится

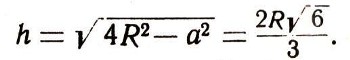
Отношение - равно

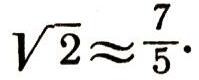
Именно такое отношение высоты балки к ширине и предписано правилами производства строительных работ.

перейти к началу страницы