Математика

Содержание раздела

Интеграл и производная

Как сделать самую большую коробку

Пусть перед нами квадратный кусок картона со стороной а. Из него надо сделать коробку без крышки. Вырежем по углам куска квадратики и согнем по линиям, отмеченным пунктиром (рис. 24). У нас получилась коробка; но много ли в нее можно положить? Это зависит от того, какие квадратики мы вырезали из этой коробки. Если они были очень маленькие, то коробка получится низкая (рис. 25) и в нее много не положишь. А если они будут слишком большие (рис. 26), то коробка получится слишком узкая и в нее тоже войдет довольно мало. Найдем, при какой стороне к вырезанного квадратика объем V(х) сделанной коробки будет наибольшим. Из рис. 24 видно, что V=x(a - 2х)²=4х³ - 4ах² + а²х. График этой функции имеет вид, указанный на рис. 27. При этом х должен лежать между 0 и a/2, так как вырезать из куска картона со стороной а четыре квадрата со стороной, большей чем a/2, нельзя. Из рис. 27 видно, что в той точке, где значение объема наибольшее, касательная идет горизонтально, т. е. образует с осью х угол, равный нулю. Но это значит, что в этой точке производная равна нулю. Таким образом, чтобы найти значение Х_mаx, при котором объем коробки будет самым большим, надо найти все значения х, при которых производная функции

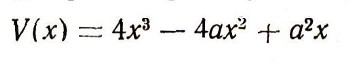
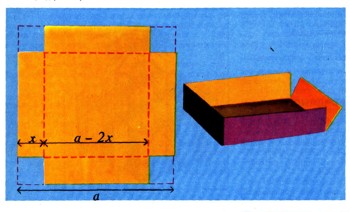
обращается в нуль; среди них обязательно будет и искомое значение x_mаx По формуле дифференцирования многочлена находим:

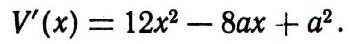
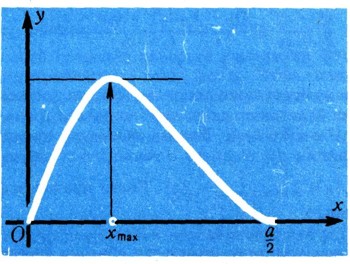
Приравниваем производную к нулю и находим два корня: х₁=a/2, х₂ =a/6. Разумеется, корень x₁=a/2 нас не устраивает: если мы вырежем квадраты со стороной a/2, то от листа картона ничего не останется. Значит, наибольшее значение объема получится, если за x_max примем оставшееся значение a/6 т. е. вырежем квадраты со стороной x= a/6 .

Объем коробки тогда будет равен 2a³/27. Сделать из данного куска картона коробку большего объема невозможно.

перейти к началу страницы