Математика
Интеграл и производная
Производная
Мы рассмотрели несколько задач из физики и геометрии. Несмотря на внешнее различие этих задач, у них было много общего. В первых двух задачах (скорость движения, скорость распада) это общее заключалось в том, что мы в обоих случаях имели скорость изменения некоторой величины: скорость движения есть скорость изменения пути с течением времени, скорость распада есть скорость изменения массы радиоактивного вещества. Но и в третьем примере мы имели некоторую скорость изменения: тангенс угла наклона касательной есть скорость изменения ординаты, когда мы перемещаемся по оси х.
Действительно, отношение y2-y1/x2-x1 представляет собой среднюю скорость возрастания ординаты при перемещении от точки х1 к точке х2, а предельное значение этого отношения (равное tg a) дает мгновенную скорость изменения ординаты.
Итак, во всех рассмотренных задачах мы имели мгновенную скорость изменения некоторой величины; этим и объясняется, что при определении этих на первый взгляд очень непохожих величин получались очень похожие формулы. Чисто математически скорость изменения можно определить следующим образом. Пусть мы имеем функцию y = f(x). Обозначим те значения, которые эта функция принимает в двух точках х1 и х2, через у1 и у2. Тогда разность y2-y1 показывает, на сколько изменилось значение рассматриваемой функции при переходе от значения х1 к значению х2, а отношение
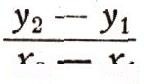
представляет собой среднюю скорость изменения функции y = f(x) на промежутке от х1 до х2. Если теперь уменьшать этот промежуток, приближая значение х2 к х1, то мы получим в пределе мгновенную скорость изменения рассматриваемой функции в точке х1; она равна:
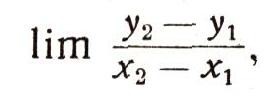
где предел берется при условии, что значение х2 приближается к х1. Эта мгновенная скорость изменения называется производной от функции y = f(x) по аргументу х в точке х1; она обозначается через f'(x1).
В этих обозначениях явно указывается, в какой точке берется мгновенная скорость изменения (т. е. производная). Есть и другие обозначения для производной, но мы их не будем указывать. Конечно, производную можно находить в различных точках, так что производная f'(x) есть опять некоторая функция от х. Теперь ясно, что рассмотренные выше задачи из физики и геометрии могут быть сформулированы с помощью производной.
Скорость движения v(t) есть производная от пути s(t) по времени:

Скорость u(t) радиоактивного распада есть производная от массы радиоактивного вещества m(t) по времени:

Наконец, тангенс угла наклона касательной к графику функции у = f(x), проведенной в точке с абсциссой х, есть производная от функции f(х):
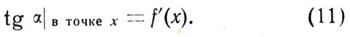
2i.SU ©® 2015