Умеете ли вы проводить касательную?

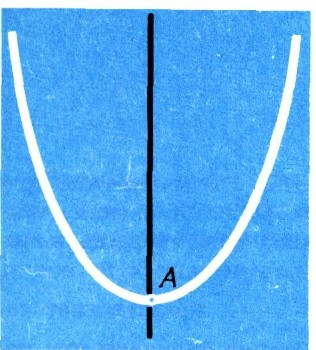
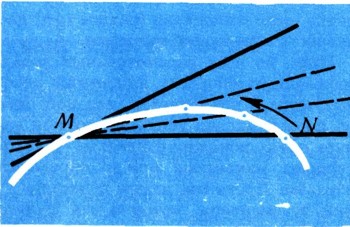
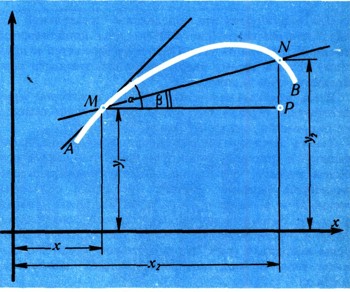
Услышав такой вопрос, вы, вероятно, вспомните построение касательной к окружности и дадите утвердительный ответ. Но речь идет о касательной к любой кривой, а не только к окружности. А в школьных учебниках не только ничего не сказано о проведении касательной к любой кривой, но даже не определяется, что это такое. Нельзя, разумеется, определять касательную как прямую, имеющую с кривой лишь одну общую точку: ось параболы пересекается с ней только в одной точке А (рис. 19), но вряд ли кто-нибудь может подумать, что это касательная. Что же такое касательная к кривой и как ее провести? Постараемся ответить на эти вопросы. Проведем через точку М, лежащую на кривой, секущую MN (рис. 20). Если теперь точку N приближать по кривой к точке М, то секущая будет поворачиваться вокруг точки М, все более приближаясь к некоторой прямой. Эта прямая и есть касательная к кривой в точке М.

Рис. 19

Рис. 20.

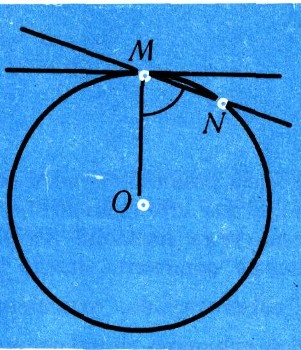
Для окружности это определение касательной совпадает с обычным (рис. 21): по мере приближения точки N к точке М угол OMN приближается к прямому углу, и потому касательная к окружности перпендикулярна радиусу.

Рис. 21

Итак, касательная - это прямая, к которой приближается секущая MN, когда точка N приближается (по рассматриваемой кривой) к точке М.

Теперь нетрудно будет описать положение касательной с помощью некоторой формулы. Для этого будем считать, что кривая А В является графиком некоторой функции y = f(x). Обозначим ординаты точек М и N через у₁и у₂, а их абсциссы - через х₁ и х₂. Рассматривая прямоугольный треугольник MPN с гипотенузой MN и катетами, параллельными осям координат (рис. 22), мы можем легко определить угол бета, под которым секущая наклонена к оси х:

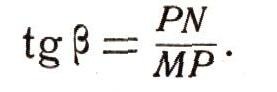
Но из рис. 22 ясно, что

Рис. 22.

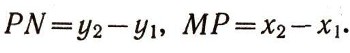
Таким образом,

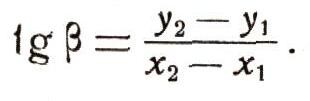
Если теперь точка N начнет по кривой А В приближаться к точке М, то секущая MN будет, поворачиваясь, приближаться к положению касательной, так что в пределе мы получим тангенс угла, под которым касательная наклонена к оси х:

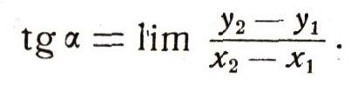
Предел берется при условии, что точка N приближается к точке М, т. е. что значение x₂приближается к х₁.

перейти к началу страницы