Чудесная формула

Тот же прием, который мы применили для приближенного вычисления площади кругового сегмента, можно, конечно, применить и для случая произвольной криволинейной трапеции; ограниченной сверху кривой CD с уравнением y = f(x) (рис. 17). Обозначим через М середину отрезка АВ и восставим в точках А, М я В ординаты AD, MN, ВС кривой CD. Длины этих ординат обозначим через у₀, у₁, у₂. Проведем через точки С, N и D дугу параболы, имеющей вертикальную ось (такую дугу можно провести всегда, и притом только одну; иногда она превращается в отрезок прямой).

Рис. 17.

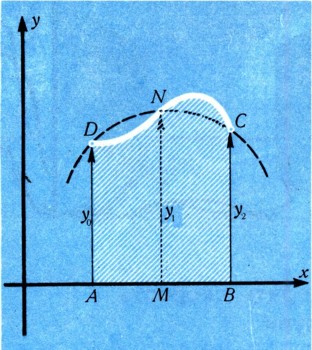
Довольно простые подсчеты, использующие формулы (5), (6), (7), показывают, что площадь, лежащая под этой дугой параболы, равна

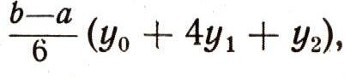
где Ъ и а - абсциссы точек В и А. Без большой ошибки можно принять, что этому же равна и площадь криволинейной трапеции ABCD, т. е. что

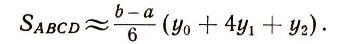
Поскольку площадь криволинейной трапеции выражается интегралом

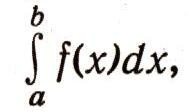
то найденная формула дает приближенное значение этого интеграла. Иными словами:

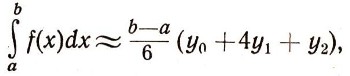
где y₀, y₁, y₂ - значения функции f(x) в точках с абсциссами а,

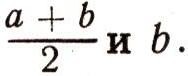
Объем любого тела можно приближенно вычислять по такой же формуле:

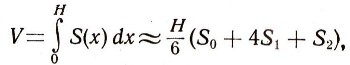
где Н - высота тела, So - площадь нижнего сечения, S₁-площадь среднего сечения, S₂-площади верхнего сечения. К этой формуле прибегают для приближенного вычисления объема дерева, стога, бочки и других фигур более или менее сложной формы. Замечательно, что для всех фигур, изучаемых в школе (призмы, цилиндра, пирамиды, конуса, усеченной пирамиды, усеченного конуса, шара, шарового слоя, шарового сегмента), эта формула дает не приближенный, а совершенно точный результат. Проверьте это утверждение.

перейти к началу страницы