Интеграл

Мы разобрали ряд задач из различных областей физики, техники, геометрии. Несмотря на внешнее различие этих задач, у них было много общего. Каждый раз для приближенного вычисления некоторой величины (объема, площади, пути и т. д.) мы получали сумму вида:

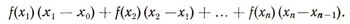
Здесь f(x) - некоторая функция, заданная на отрезке от а до b, а х₀ = а, х₁, ..., х_п-1, х_п = b - точки на этом отрезке. Например, при вычислении пути функция f(x) была скоростью в момент времени х (только время мы раньше обозначали буквой t, а не х, что, конечно, несущественно), а было равно нулю, a b равнялось времени Т движения автомобиля.

Суммы такого вида встречаются в математике и ее приложениях очень часто. Их называют интегральными суммами. Такие суммы дают значение искомой величины только приближенно. Но если мы будем брать точки X₀, Х₁, ..., х_n все гуще и гуще на отрезке от а до b, то интегральные суммы будут приближаться к некоторому числу, а именно к точному значению искомой величины. Это число называется интегралом от функции f(x) на отрезке от а

до bи обозначается через

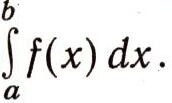
Таким образом,

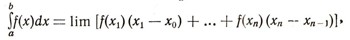
где предел (lim) берется при условии, что число промежутков неограниченно увеличивается, а их длины стремятся к нулю. В самом обозначении

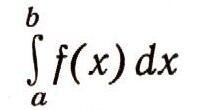
сохраняются воспоминания об интегральной сумме, из которой получается интеграл. В Италии букву 5 часто пишут в виде интеграла. Поэтому сам знак интеграла есть просто первая буква латинского слова summa (сумма). Вслед за знаком интеграла указывается, что суммировались выражения f(x_k)(х_k-x_k-1)- Только вместо разности x_k-x_k-1 пишут d_x, где d - первая буква латинского слова differentia (разность). Понятие интеграла является одним из основных в математике. Пользуясь этим понятием, можно записать многие полученные ранее формулы гораздо короче и не приближенно, а точно. Например, формула объема любого тела принимает вид:

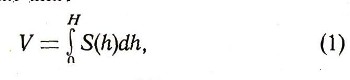
где Н - высота этого тела, a S(h) - площадь сечения, проведенного параллельно основанию тела на высоте h от основания. Формулу площади фигуры, можно записать в виде:

где f(x) - высота кривой CD в точке с абсциссой х. Путь, пройденный за промежуток времени от 0 до Т, выражается через скорость v(t) по формуле:

перейти к началу страницы