Объем тела

На общем рисунке изображены и другие тела вращения: чашка, бутыль, подсвечник, графин, яйцо, волчок. Для нахождения объема любого тела вращения пригоден прием, примененный нами для вычисления объема лимона. Пусть фигура ABCD вращается вокруг стороны АВ. Разрежем получающееся тело вращения на тонкие ломтики и каждый ломтик заменим цилиндром. Тогда легко сможем найти объем получающегося ступенчатого тела (рис. 6). Для этого надо знать, как меняется площадь сечения с высотой (рис. 7).

Рис. 6

Рис. 7

Рис. 8

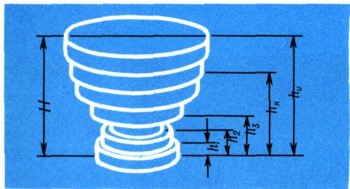
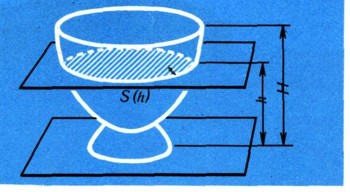
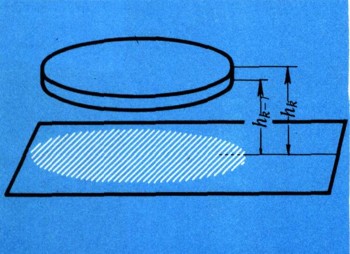
Пусть площадь сечения, проведенного на высоте h, равна S(h). Предположим, кроме того, что тело разрезано на п ломтиков сечениями, проведенными на высотах h₀, h₁, ..., h_n над плоскостью нижнего основания (плоскость нижнего основания совпадает с сечением на высоте h₀, а плоскость верхнего - с сечением на высоте h_n, т. е. h₀ = 0, h_n = H (см. рис. 6)). Площадь сечения на высоте hk равна S(h_k). Поэтому объем цилиндра, которым мы заменяем k-й ломтик (рис. 8), будет равен S(h_k) (h-h_k-1) (так как его высота h_k -h_k-1). Складывая объемы цилиндров, получим объем всего ступенчатого тела:

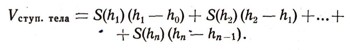
Чем тоньше будут ломтики, тем ближе объем ступенчатого тела к объему тела вращения. Но на рисунке есть и фигуры, не являющиеся телами вращения (кувшин, батон). Объем любого тела можно найти таким же образом, если известно, как меняется площадь тела с высотой сечения. Например, для того чтобы вычислить объем проектируемого корабля, достаточно иметь чертежи (выполненные в определенном масштабе) поперечных размеров корабля. По этим чертежам надо найти площадь каждого разреза (как вычислить площади сложных фигур, мы расскажем ниже), после чего указанная выше формула даст приблизительное значение объема корабля. Разумеется, таким же приемом можно находить объемы газгольдеров, водохранилищ и других тел.

перейти к началу страницы