Вынужденные колебания

Рассмотрим снова гирю, качающуюся на пружине. Если не мешать ей качаться, то она будет совершать колебания с определенной частотой w. Эта частота называется собственной частотой колебания гири. Совсем по-другому будут выглядеть колебания гири, если мы будем раскачивать ее. Пусть раскачивающая сила сама изменяется по синусоидальному закону, т. е. тащит гирю то вверх, то вниз. Тогда гиря будет совершать колебания, получающиеся при сложении двух колебаний. Одно из них происходит с собственной частотой колебания гири, а второе -с частотой раскачивающей силы. Пусть в начале колебания гиря находится в состоянии покоя и раскачивающая сила изменяется по закону: F = Asin бета*t. Тогда закон движения гири выразится формулой:

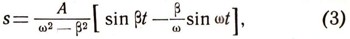
где w - собственная частота колебаний гири. График пути гири имеет уже довольно сложный вид. Дело в том, что функции sin бета*t и sin wt меняются с разной частотой. Поэтому иногда два колебания, в которых участвует гиря, направлены в разные стороны (так будет, например, в начале колебания) и гасят друг друга. Иногда же они направлены в одну сторону, и тогда они усиливают друг друга.

Наибольшая амплитуда колебания равна примерно

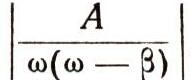
Отсюда видно, что если бета мало отличается от (о (т. е. частота раскачивающей силы мало отличается от собственной частоты колебаний гири), то амплитуда колебаний может стать очень большой

(у дроби

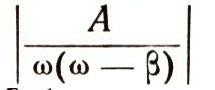
знаменатель будет маленьким).

Если w = бета (т. е. если мы раскачиваем гирю в такт ее собственным колебаниям), то формула (3) уже неприменима. В этом случае закон движения таков:

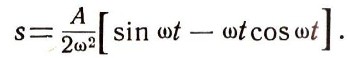
Размах колебаний с течением времени увеличивается, и гиря может разорвать пружину. Это явление называют резонансом.

перейти к началу страницы