Затухающие колебания

До сих пор, говоря о колебаниях маятника, гири, качающейся на пружине, и т. д., мы пренебрегали сопротивлением воздуха. На самом деле из-за сопротивления воздуха амплитуда колебаний становится все меньше и меньше, колебания затухают. Отклонение точки, совершающей затухающие колебания, выражается такой формулой:

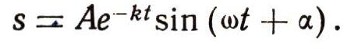
Так как множитель е^-kt уменьшается с течением времени, то размах колебаний становится все меньше и меньше. После каждого полного колебания амплитуда уменьшается в

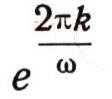
раз. Число

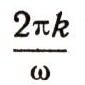
называют логарифмическим декрементом затухающего колебания. Чем больше логарифмический декремент, тем быстрее затухают колебания. Через некоторое время они станут такими маленькими, что приборы покажут полную остановку тела. График затухающего колебания изображен на рис. 11.

Рис. 11 График затухающего колебания.

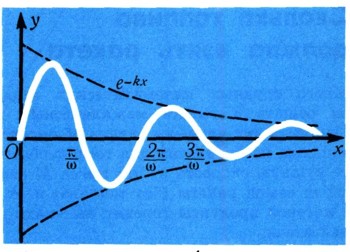
Если сопротивление среды очень большое (скажем, если маятник качается не в воздухе, а в масле), то колебаний не будет совсем - выведенный из положения равновесия маятник медленно будет опускаться, приближаясь к положению равновесия. В этом случае закон его движения задается следующей формулой :

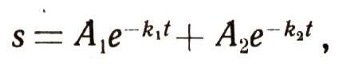
где числа А₁ и A₂ зависят от начального положения и начальной скорости маятника. При электрических колебаниях также происходят затухающие колебания из-за наличия сопротивления цепи.

перейти к началу страницы