Математика
Функции
Гармонические колебания
Мы рассмотрели несколько примеров из физики и техники, в которых так или иначе встречается показательная функция. Сейчас перейдем к рассмотрению примеров, связанных с тригонометрическими функциями.
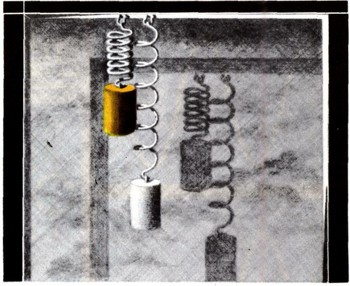
Начнем с гармонических колебаний. Возьмем, например, гирю, подвешенную на пружине (рис. 7), и толкнем ее вниз. Гиря начнет колебаться вниз и вверх. Как показывают расчеты, отклонение гири от положения равновесия выражается формулой:
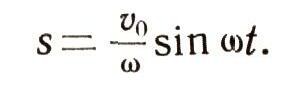
Здесь V0 - скорость, с которой мы толкнули гирю,
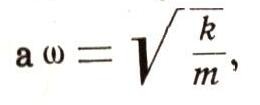
где т - масса гири и k - жесткость пружины (сила, которая нужна, чтобы растянуть пружину на 1 см).
Колебания, происходящие по закону

называют синусоидальными или гармоническими, а график функции (1) - синусоидой. Мы можем получить представление о таких колебаниях, следя за движением равномерно вращающейся точки и наблюдая это движение одним глазом сбоку (так, что глаз наблюдателя находится в плоскости вращения). Нам будет казаться, что точка не вращается, а движется то в одну сторону, то в другую. Такую картину наблюдают астрономы, следя за движением спутников Юпитера, когда Земля находится в плоскости орбиты этих спутников.
Число А, называемое амплитудой синусоидального колебания, показывает размах этого колебания, а число о), называемое частотой колебания, показывает, сколько колебаний происходит за 2л секунд (т. е. примерно за 44/7 с). Через каждые - секунд гиря будет возвращаться в исходное положение. Поэтому период ее колебания равен 2Пи/w.
Если мы сначала оттянем гирю на s0 см, а потом толкнем ее со скоростью v0, то она будет совершать колебания по более сложному закону:
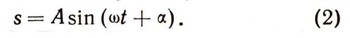
Расчеты показывают, что амплитуда А этого колебания равна
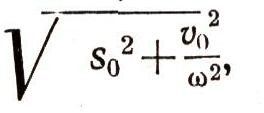
а число таково, что
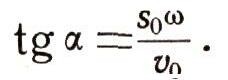
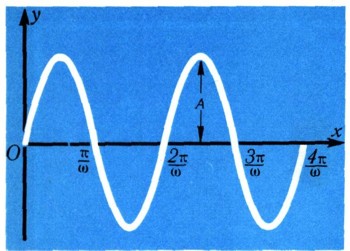
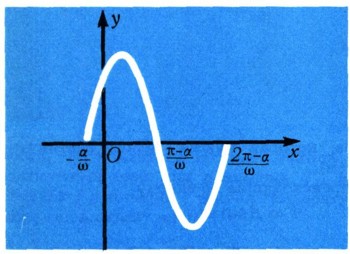
Из-за слагаемого а это колебание отличается от колебания s = Asinwt. На рис. 8 и 9 изображены графики обоих колебаний. График колебания (2) получается из графика колебания (1) сдвигом влево на a/w Число а называют начальной фазой.
2i.SU ©® 2015