Прогиб балки

Прогиб балки зависит не только от ее жесткости, но и от длины балки, распределения нагрузки, от того, заделаны ли в стену оба конца балки или только один, и т. д. Чтобы найти наибольший прогиб балки, надо знать форму, которую она принимает после изгиба. Возьмем балку длины l, заделаем оба ее конца в стены и положим на нее равномерно распределенную нагрузку Q. Тогда прогиб у в точке, находящейся на расстоянии х от левого конца балки (рис. 3), выражается формулой:

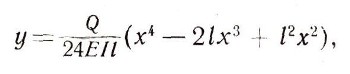
т. е. многочленом четвертой степени. График этого многочлена изображен на рис. 3. Ясно, что самый большой прогиб балки будет в середине, т. е. при x = l/2. Он равен

Рис. 3 Сплошной белой линией показан (в значительно увеличенном по оси Оу масштабе) прогиб балки, заделанной на концах, под действием равномерно распределенной нагрузки.

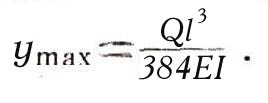
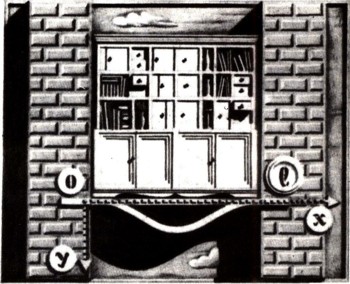
Балки, на которые опираются балконы, заделывают в стену лишь одним концом, второй оставляют свободным. Такие балки называются консольными. Форма равномерно нагруженной консольной балки (рис. 3а) выражается уравнением:

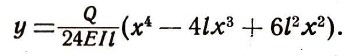
Здесь уже наибольший прогиб будет на свободном конце балки, при х=l. Он в 48 раз больше, чем для такой же балки, оба конца которой заделаны.

Рис. 3а. Сплошной белой линией показан (в значительно увеличенном по оси Оу масштабе) прогиб консольной балки под действием равномерно распределенной нагрузки.

Рис. 4. Сплошной белой линией показан (в значительно увеличенном по оси Оу масштабе) прогиб балки, концы которой свободно лежат на опорах, под действием средоточенной нагрузки.

перейти к началу страницы