Криволинейные координаты на любой поверхности. Общая идея координат

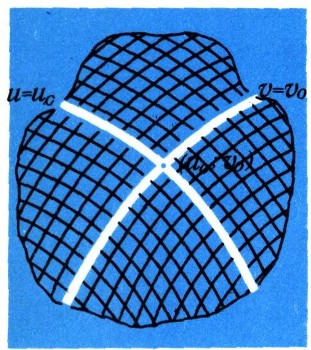
На любой поверхности можно установить координатную систему, определяя положение точки на ней опять-таки двумя числами. Для этого каким-либо способом покроем всю поверхность двумя семействами линий так, чтобы через каждую ее точку (быть может, за небольшим числом исключений) проходила одна, и только одна, линия из каждого семейства. Теперь надо лишь снабдить линии каждого семейства числовыми пометками по какому-нибудь твердому правилу, позволяющему по числовой пометке находить нужную линию семейства (рис. 22). Координатами точки М поверхности служат числа и, V, где и - числовая пометка линии первого семейства, проходящей через М, к v - пометка линий второго семейства. По-прежнему будем писать: М (и; v); числа и, V называются криволинейными, координатами точки М. Сказанное станет совсем ясным, если за примером обратиться к сфере. Ее всю можно покрыть меридианами (первое семейство); каждому из них соответствует числовая пометка, а именно значение долготы и (или ф). Все параллели образуют второе семейство; каждой из них отвечает числовая пометка - широта v (или 6). Через каждую точку сферы (исключая полюсы) проходит только один меридиан и одна параллель.

Рис. 22

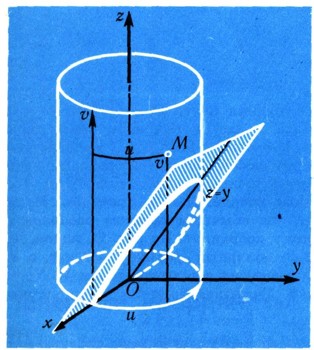
В качестве еще одного примера рассмотрим боковую поверхность прямого круглого цилиндра высоты Я, радиуса а (рис. 23). За первое семейство примем систему его образующих, одну из них примем за начальную. Каждой образующей припишем пометку и, равную длине дуги на окружности основания между начальной образующей и данной (дугу будем отсчитывать, например, против часовой стрелки). За второе семейство примем систему горизонтальных сечений поверхности; числовой пометкой vбудем считать высоту, на которой проведено сечение над основанием. При надлежащем выборе осей х, у, z в пространстве будем иметь для любой точки М (х; у; z) нашей поверхности:

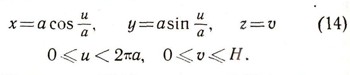
(Здесь аргументы выражены не в градусах, а в радианах.) Эти уравнения можно рассматривать как параметрические уравнения поверхности цилиндра.

Задача 9. По какой кривой надо вырезать кусок жести для изготовления колена водосточной трубы, чтобы после надлежащего изгибания получился цилиндр радиуса а, усеченный плоскостью под углом 45° к плоскости основания?

Рис. 23.

Решение. Воспользуемся параметрическими уравнениями поверхности цилиндра:

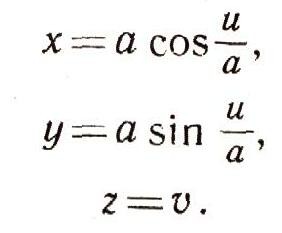
Секущую плоскость проведем через ось Ох, ее уравнение z = у. Комбинируя его с только что написанными уравнениями, получим уравнение

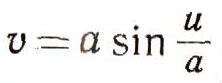
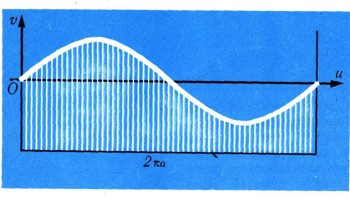
линии пересечения в криволинейных координатах. После развертки поверхности на плоскость криволинейные координаты и и v превратятся в декартовы. Итак, кусок жести должен быть сверху очерчен по синусоиде v = asin u/a. Здесь u и v уже декартовы координаты на плоскости (рис. 24).

Рис. 24

Как в случае сферы и цилиндрической поверхности, так и в общем случае задание поверхности параметрическими уравнениями влечет за собой установление на поверхности криволинейной системы координат. Действительно, выражение декартовых координат х, у, z произвольной точки М (х; у; z) поверхности через два параметра и, и (это в общем случае записывают так:

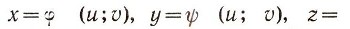
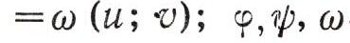
- функции двух аргументов) дает возможность, зная пару чисел и, V, найти соответствующие координаты х, у, z, а значит, положение точки М на поверхности; числа и, v служат ее координатами. Давая одной из них постоянное значение, например, и = и₀, получим выражение х, у, z через один параметр v, т. е. параметрическое уравнение кривой. Это координатная линия одного семейства, ее уравнение и = и₀. Точно так же линия v = v₀ -координатная линия другого семейства.

перейти к началу страницы