Координаты на сфере

Положение точки на сфере удобнее всего задавать так, как это делается в географии. На данной сфере радиуса R выберем какие-нибудь две диаметрально противоположные точки, одну из них - N назовем условно северным полюсом, другую - S - южным. Какой-нибудь из "меридианов" (кратчайший путь по сфере из S в N) назовем начальным меридианом; проходящую через центр О сферы и перпендикулярную оси SN плоскость назовем экваториальной, а пересечение ее со сферой - экватором, на экваторе изберем направление, скажем, против часовой стрелки, если смотреть из N. Положение любой точки М на сфере определяется двумя координатами, одна из них, назовем ее долготой, - угол ф между плоскостью начального меридиана и плоскостью, проходящей через М и ось SN (угол должен отсчитываться в направлении, соответствующем выбранному на экваторе). Широтой точки М будем называть угол между радиусом ОМ и плоскостью экватора (0 считается положительным для точек северного полушария и отрицательным для южного). Будем писать: М (ф; 6) , ставя на первое место долготу, на второе - широту.

Пример. Проверьте правильность координатного обозначения точек на рис. 21.

Все точки с одинаковой долготой ф₀ заполняют меридиан, уравнение которого поэтому ф=ф₀. Все точки с одинаковой широтой 6о заполняют параллель 0 = 0₀. Уравнение, связывающее текущие координаты ф и 0, определяет, как и в плоской геометрии, кривую; неравенство, соответствующее этому уравнению, определяет одну или несколько областей, на которые эта кривая разделяет сферу. Так, неравенство 0<0 определяет южную полусферу, 0>0 -северную; уравнение 0=0 есть уравнение экватора.

Рис. 21.

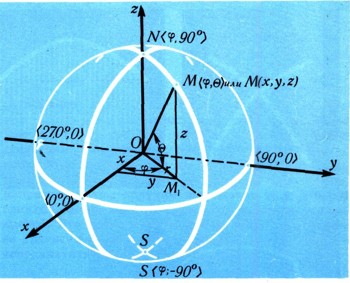
Если сферу отнести к декартовым координатам в пространстве, приняв центр О сферы за начало, ось SN - за ось z, ось х направив через точку <0°; 0°> , ось у - через <90°; 0°> , то декартовы координаты х, у, г любой точки М сферы легко выразить через долготу и широту этой точки. Для этого выразим сначала координаты ее проекции М₁ на плоскость Оху, где обычным образом расположим полярную систему координат. Из рис. 21 видно, что для M₁ (х; у; 0) полярный радиус r = Rcos0, а полярный угол ср совпадает с долготой точки М. Кроме того, z = R sin 6. Учитывая формулы (11), получим:

По этим формулам вычисляют декартовы координаты точки М (х; у,z), если известны ср и 9.

На эти же формулы можно взглянуть и с другой точки зрения. Будем считать ср и 6 переменными, придавая им всевозможные значения в естественных пределах 0°<ф<360°, -90°=<0=<+90°; тогда точка М (ф;0) будет перемещаться по сфере, занимая всевозможные положения. Это напоминает параметрические уравнения линии, в которых декартовы координаты х, у, я выражены через один переменный параметр t. Разница лишь в том, что теперь х, у, z выражены через два параметра, поэтому получается не линия (одномерное образование), а поверхность (образование двумерное). Подобные уравнения называют параметрическими уравнениями поверхности; переменные параметры чаще всего здесь обозначают буквами и и v. Итак, параметрические уравнения сферы запишем в виде:

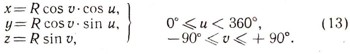
Если из этих уравнений исключить параметры и, V (для этого проще всего возвести уравнения (13) в квадрат и сложить), получим обычное уравнение сферы: х²+y² + z² = R².

перейти к началу страницы