Полярные координаты

При решении многих задач удобнее пользоваться так называемыми полярными координатами: на плоскости выбирают неподвижную точку О (полюс) и выходящий из нее луч ОР (полярная ось). Положение точки М в этом случае определяется двумя числами: ее расстоянием r от полюса и углом у = угол РОМ (рис. 16). Числа r (полярный радиус) и ср (полярный угол) называются полярными координатами точки М.

Рис. 16

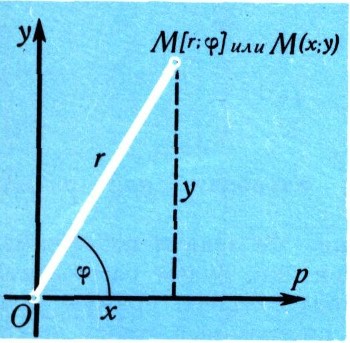
Часто оказывается полезным рассматривать на плоскости полярную систему координат вместе с декартовой. Рассмотрим такое расположение, когда полюсом служит начало декартовой системы, а полярной осью - ось абсцисс (рис. 16); рисунок сам подсказывает связь между полярными и декартовыми координатами точки:

Эти формулы позволяют вычислить декартовы координаты, когда известны полярные. Пример. Выяснить форму кривой

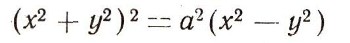
(она называется лемнискатой). Исследовать ее форму непосредственно по написанному уравнению не так легко. Перейдем к полярным координатам. Заменив х. и у по формулам (11), получим: r* = a²r² (cos²ф - sin²ф). Или, сократив на r² (при этом могла бы потеряться лишь одна точка г = 0), получим: r² = a²cos2ф, или r=+a корень из cos2ф. По этому простому уравнению легко построить нашу кривую. Кривая строится по точкам (рис. 17). Даем ср различные значения, например: ф = 0°, ±15°, ±30°, ±45°, ±135°. Вычисляем соответствующие r=a, a корень из ³/₄, a корень из 1/2, 0, 0. При значениях ср между 45° и 135°, а также между 225° и 315° косинус отрицателен и поэтому r мнимо: у кривой нет точек с такими значениями полярного угла.

Рис. 17

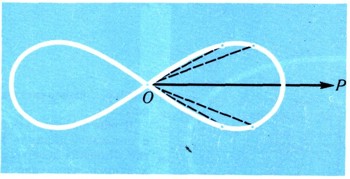
Точки, у которых полярный радиус имеет постоянное значение r = r₀, образуют окружность радиуса r₀, описанную вокруг полюса. При постоянном значении угла ф, ф = ф'о, получается луч, выходящий из полюса и наклоненный под углом ф₀ к полярной оси. Полученные таким образом (т. е. при постоянном значении одной координаты) линии называются координатными, (рис. 18). В декартовой системе координатные линии - прямые, параллельные осям. Спираль Архимеда . Эта кривая задается в полярных координатах уравнением r=С_ф, где С-постоянная (рис. 19).

Рис. 18

Рис. 19

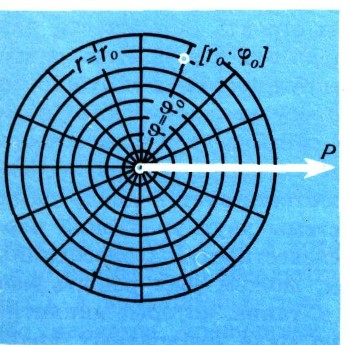
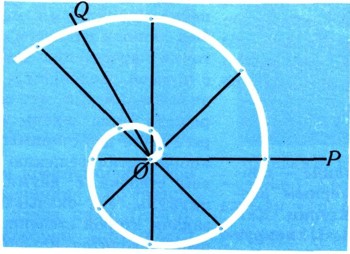
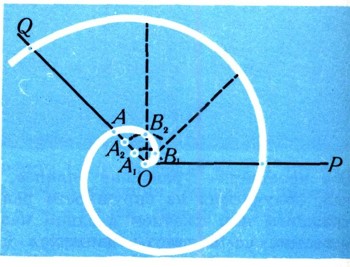
При помощи этой кривой любой угол можно делить на произвольное число (например, на три -трисекция угла) равных частей. Вот как это делается (рис. 20). Пусть на листе бумаги начерчена спираль Архимеда, выходящая из полюса О полярной системы координат, полярная ось ОР служит для спирали касательной. Перенесем на этот чертеж заданный нам для разделения на п равных частей угол так, чтобы его вершина совпадала с полюсом, одна сторона - с полярной осью ОР, а другая его сторона - OQ легла в сторону возрастания полярного угла ф (против часовой стрелки). Обозначим первую (считая от О) точку пересечения этой другой стороны с нашей спиралью буквой А; затем разделим отрезок ОА на п равных частей (что, как .вы знаете, легко делается циркулем и линейкой) и проведем через точки А₁, А₂, - деления отрезка ОА дуги окружностей с общим центром О до пересечения со спиралью; наконец, полученные точки В₁, В₂, ... пересечения соединим с полюсом - и данный угол POQ разделен на п равных частей! Докажите это сами.

Рис. 20

перейти к началу страницы