Математика

Содержание раздела

Функции

Аналитическое решение геометрических задач

При решении геометрической задачи аналитическим методом прежде всего выбирают систему координат (от удачного выбора ее зависит простота вычислений). Затем находят в этой системе координаты заданных точек и уравнения заданных прямых, окружностей и т. д. Этим задача переводится на аналитический язык и превращается в задачу аналитической геометрии.

Пример 1. Доказать, что три высоты треугольника ABC всегда пересекаются в одной точке. Пусть ось Оу проходит по высоте ОС, а ось Ох -по соответствующему основанию А В. Координатное обозначение вершин: А ( - р; 0), В (q; 0), С (0; h) (h - высота, р, q - проекции сторон С А и С В на основание). По формуле (4) составляем уравнения боковых сторон:

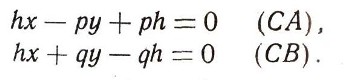
(Сделайте проверку: ( - р; 0) лежит на С А, (0; h) - тоже.) Составляем уравнения боковых высот: px + hy = pq, qx - hy=-pq (см. задачу 8). Точка пересечения (0; pq/h) найденная совместным решением их уравнений, очевидно, лежит на третьей высоте, так как ее абсцисса равна нулю.

Пример 2. (Эллипс.) Выяснить, какую кривую опишет точка тонкой прямолинейной палочки, скользящей своими концами по неподвижным взаимно перпендикулярным прямым Ох и Оу. Примем эти прямые за оси координат. Расстояния точки от концов палочки обозначим через а и b (постоянные числа, так как точка по палочке не двигается)

Обозначим через t (переменный) угол, образованный палочкой с отрицательным направлением оси Ох. На рис. 14 видно, что

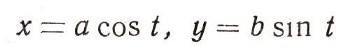
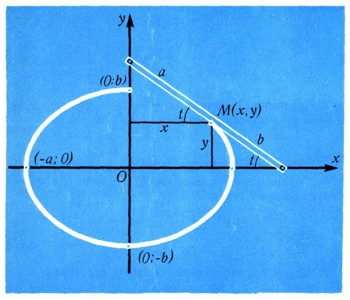
Эти два уравнения можно рассматривать как особый вид уравнений кривой. Здесь связь между х и у задана при помощи вспомогательного переменного (параметра) t. Такие уравнения кривой называются параметрическими. По ним построение кривой делают так: дают произвольные значения параметру t, каждый раз вычисляя соответствующие значения X и у, что определяет точку кривой. Так, точка за точкой, можно построить сколько угодно точек кривой. Если вы хотите получить обычное ее уравнение, следует исключить из параметрических уравнений параметр t (не всегда это легко сделать!), т. е. составить их следствие, не содержащее t. В данном случае, деля эти уравнения: первое - на а, второе -на b, возводя в квадрат и складывая, получим?

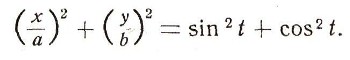
или

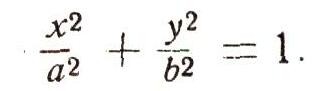
Это простейшее уравнение эллипса. Эллипс - кривая, получаемая из окружности равномерным растяжением или сжатием в одном направлении. Как известно, по эллипсам движутся планеты вокруг Солнца (первый закон Кеплера), Луна и искусственные спутники вокруг Земли.

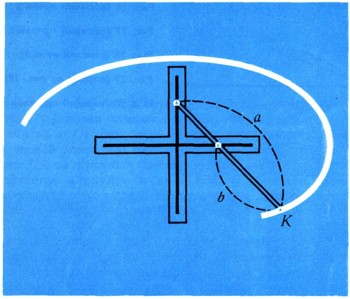
Эллипсограф. Из рассмотренной только что задачи вытекает конструкция прибора для черчения эллипсов (эллиптический циркуль, или эллипсограф). Для этого нужно лишь к подвижной палочке прикрепить карандаш, который можно было бы закреплять винтом в различных положениях на палочке. Этот карандаш при описанном выше движении палочки вычертит эллипс, полуоси которого a, b зависят от того, в какой точке палочки закреплен карандаш. Из уравнения (10) следует, что середина палочки описывает окружность, ведь для середины а = b! На рис. 15 показан эллипсограф несколько иной конструкции.