Окружность

Как известно, окружностью называется множество точек плоскости, находящихся от заданной точки С этой плоскости (центра) на заданном расстоянии R (радиус). Запишем это определение аналитически относительно декартовой системы координат. Пусть С (а; b). Тогда для любой точки Р (х; у) окружности PC = R, т. е.

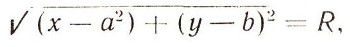
или

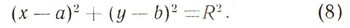
Это и есть (общее) уравнение окружности. Раскрыв в нем скобки

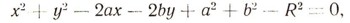
убеждаемся, что это есть частный случаи общего уравнения второй степени относительно х и и:

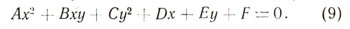
В нашем случае A = С=1, В = 0. Оказывается, что всякое уравнение второй степени относительно декартовых координат к, у, в котором коэффициенты при X² и у² равны (и по абсолютной величине и по знаку: А = С), а коэффициент при ху равен нулю (В = 0), либо является уравнением некоторой окружности (быть может, нулевого радиуса), либо ни одна (действительная) точка плоскости ему не удовлетворяет.

Задача 8. Построить окружность 2х²+2у² + 3у = 0.

Пишем уравнение так:

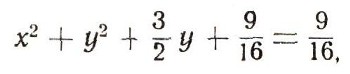
или

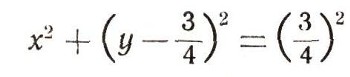
Сравнивая с общим уравнением окружности, видим, что а = 0, b = -3/4; R =3/4

Теперь легко выполнить построение. Если в общем уравнении 2-й степени А не равно С или В не равно 0, то такое уравнение уже не будет уравнением окружности. Оказывается, возможны здесь только такие линии: парабола, эллипс (см. ниже, пример 2), гипербола или (если левая часть уравнения разлагается на множители первой степени) пара прямых. Все они называются линиями, второго порядка. Впрочем, бывает и так, что ни одна точка плоскости уравнению не удовлетворяет, например: 2х²+3у²+1=0 (мнимый эллипс).

перейти к началу страницы