Основные задачи на прямую

Как мы видели, прямая однозначно определяется ее уравнением. Поэтому уравнение прямой может служить как бы ее "именем"; постоянно говорят: "Прямая Ax + By + C =0"; это значит, что прямая задана уравнением Ах + Ву + С = 0.

1) Построение прямой по ее уравнению. Чтобы построить прямую по ее уравнению, проще всего найти какие-нибудь две точки, удовлетворяющие этому уравнению; построив их, провести через них прямую. Пример. Построить прямую 2х - Зу + 8 - 0. Этому уравнению удовлетворяют точки (-4; 0), (-1; 2), (5; 6), .... Строим какие-нибудь две из них (лучше не слишком близкие, иначе проведение через них прямой по линейке не будет достаточно точным), например (-4; 0) и (5; 6), и соединяем линейкой.

2) Даны две различные точки A₁[x₁;y₁] и А₂[х₂;у₂] Найти прямую A₁A₂. (Найти ее уравнение.)

Убедимся, что искомое уравнение можно записать так:

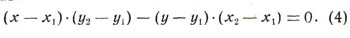
Прежде всего это уравнение первой степени относительно текущих координат х, у, значит, оно есть уравнение прямой. Подставляя вместо текущих координат х и у сначала х₁ и y₁ а затем х₂ и y₂, убеждаемся каждый раз, что уравнение обращается в тождество, значит, эта прямая проходит и через точку (х₁; y₁), и через точку (х₂; y₂).

Обычно уравнение (4) записывают в более удобной для запоминания форме:

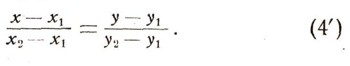
Однако последняя перестает служить, если х₁ = у₂или y₁= у₂.

3) Даны две прямые: Ах + Ву + С = 0 и А'х + + В'у + С' = 0. Найти точку их пересечения.

Точка пересечения лежит на той и на другой прямой, следовательно, ее координаты должны удовлетворять обоим уравнениям. Итак, для нахождения их надо решить совместно эти уравнения (система двух уравнений с двумя неизвестными).

4) Условие параллельности. Как следует из сказанного ранее, угловой коэффициент k характеризует направление прямой, поэтому равенство угловых коэффициентов двух прямых означает их параллельность. Так как k-=A/B, то условие параллельности (k = k') прямых Ах + Ву + С = 0 и А'х + В'у.+ С' = 0 может быть записано и так:

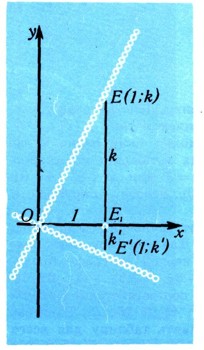
5) Условие перпендикулярности. Бели прямые перпендикулярны, то углы аи а', образуемые ими с осью Ох, разнятся на 90°; a' = а + 90°, поэтому их угловые коэффициенты k и k' удовлетворяют равенству kk' = - 1. Это легче всего усмотреть из рис. 13: на нем треугольник ОEЕ' прямоугольный, k и -k' служат проекциями катетов на гипотенузу, поэтому их произведение равно квадрату высоты: k(-k')=OE²=1. Иначе условие перпендикулярности пишут в виде k' = -1/k или, в силу равенств к

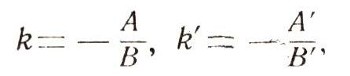
виде АА' + ВВ' = 0. (6)

Рис. 13.

Задача 7. Через точку (2; -3) провести прямую, перпендикулярную прямой 4х - 3y + 2 = 0.

Решение. Для изменения направления на перпендикулярное достаточно (выполняя условие (6)) поменять местами коэффициенты Л и в и у одного из них изменить знак: Л = 4, В= - 3; теперь возьмем А'= +3, В' = 4. Уравнение искомой прямой уже можно написать: Зх + 4у + С' = 0. Неизвестный пока член С' определится из требования, чтобы данная точка (2; -3) лежала на этой прямой 3.2 + 4.(-3)+С' = 0, или С' = 6.

Ответ: Зx + 4y + 6 = 0.

6) Расстояние между точкой и прямой. Рассмотрим частный случай этой задачи: найти длину р перпендикуляра из начала О (0; 0) на прямую Ах+Ву+С=0. Решение удобно вести по такой схеме.

1. Найти уравнение перпендикуляра из О (0; 0) на Ах + Ву.+ С = 0 (см. задачу 7).

Ответ: Вх - Аy = 0.

2. Проекция О' начала О на данную прямую получается совместным решением уравнений:

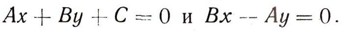
Ответ:

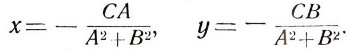
3. Остается найти искомое расстояние р как расстояние между О и О':

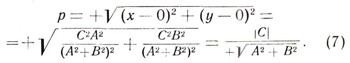
В общем случае задача: "Найти расстояние d от точки Р₀ (X₀; у₀) до прямой Ах + Ву + С = 0" - может быть решена тем же путем. В результате получим:

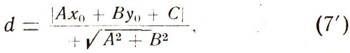
т. е. расстояние от точки (х₀; у₀) до прямой Ах+Ву+С=0 равно частному от деления абсолютной величины результата подстановки в левую часть уравнения прямой координат точки (х₀; y₀) на "нормирующий" корень A²+ В².

Все приведенные в пунктах 1), 2), ..., 6) задачи следует научиться решать совершенно свободно, так сказать, "с закрытыми глазами".

перейти к началу страницы